Беседы с Жаком Лаканом. Интервью Жан-Пьера Пети. Часть 3: Поверхность Боя
Жан-Пьер Пети: Вернувшись в
После того, как я осознал, если не свое состояние, то, по крайней мере, мой внешний вид, мне стало легче справиться с ситуацией, в первую очередь — реакцией пассажиров моего купе. Очевидно, было бесполезно пытаться что-либо им объяснить. Мне вспомнилась фраза из романа «Огромный зверь». Это история о том, как однажды маленький ребенок обнаруживает древнего дракона, живущего в иссыхающем болоте. Тогда мальчик решается вести его вдоль Сены, чтобы тот мог добраться до
Лихнерович был в восторге от моего визита. По пути я выяснил, как расположить меридианы поверхности Боя и предположил, что их можно описать как семейство эллипсов. Это открытие впоследствии позволило Апери построить первое неявное уравнение этой поверхности.
Лакан тепло меня принял. Он не прекращал повторять: «Вы очень добры!». Визит Деда Мороза, вероятно, не доставил бы ему большего удовольствия. Картонная модель позволила ему лучше понять объект (рисунок 11), хорошо расположить его уникальный «полюс». Это односторонний объект. Если его снабдить сеткой, системой меридианов и параллелей, то появится уникальная «особенность сетки» (полюс), которую я указал. Лакан решил переселить туда объект маленькое, а или символический фаллос. Признаюсь, мои знания в области анатомии человеческого мозга недостаточно хороши, чтобы оценить эту деталь. Он без труда определил экватор поверхности. Он несколько раз провел по этой линии пальцами, и взгляд его загорелся.
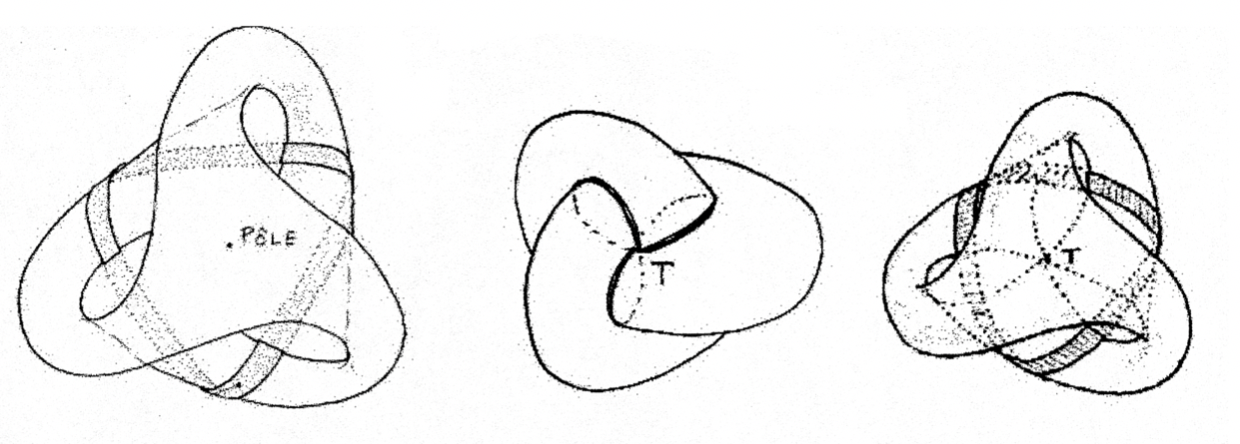
— А вот и линия разреза [le refend].
— Что?
— Линия разреза (лента Мебиуса с тремя полуоборотами, тянущаяся вдоль экватора). Вы принесли модель, которая была мне нужна.
— Рад оказать вам эту услугу…
Мне показалось это весьма занимательным. Я ничего не понимал в его рассказах, но казалось, что он удовлетворен этим «новым вкладом геометрии в психоанализ». Мы долго возвращались к «несуществованию тройной точки» в качестве геометрического объекта, свойственной [intrinsèque] поверхности как таковой. Возможно, Лакан хотел убедиться, что на этот раз у него в руках оказалась правильная поверхность, наделенная уникальной сингулярностью. Он, вероятно, не переварил ту плохую шутку, которую с ним сыграл кросс-кап с этим неожиданным возрождением своей второй куспидальной точки. Я был поражен его ловкостью в понимании довольно-таки абстрактных понятий вроде линии самопересечения. После того, как он закончил осмотр, поместил свой сингулярный объект в нужное место и установил его «линию разреза» или «линию рассечения», я точно уже не помню, он, в конце концов, повернулся ко мне со словами:
— Значит, про эту тройную [trifoliée] кривую самопересечения (которая самопересекается в точке тройной Т) мы забываем?
— Верно, мы про нее забываем.
Фабрис Гийо: Уважаемый Жан-Пьер Пети, в этой точке я позволю себе прервать ход вашего повествования и предложить вставить в текст некоторые элементы, которые, благодаря рисункам, взятым из одной стати, размещенной среди прочих на вашем сайте и дополненных комментариями, покажут те причины, по которым Лакан смог найти в ходе вашей встречи идеальную аналогию между его формализацией фундаментального фантазма и математическими характеристиками топологической поверхности, в данном случае — поверхности Боя. Вот что вы там пишете:
В Топологиконе [1] мы находим небольшой комикс, который показывает, как лента Мебиуса с тремя полуоборотами может трансформироваться в поверхность Боя (рисунок ниже). Предпоследнее изображение следующего номера показывает эту поверхность, минус диск. Чтобы завершить трансформацию, достаточно просто добавить к ней диск.
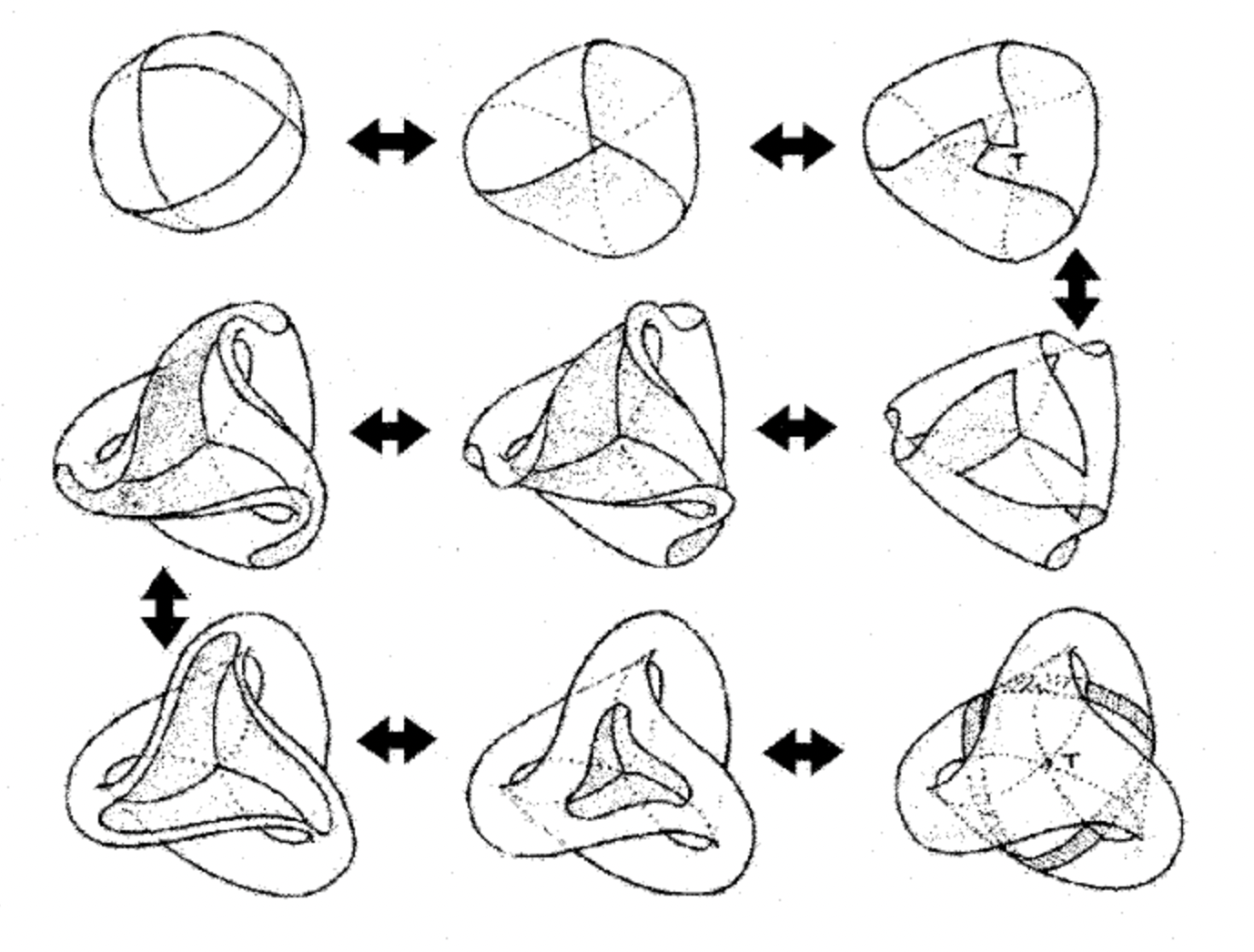
И, наоборот, можно было бы начать с диска и вырастить его путем самопересечения — до тех пор, пока он не склеится по ленте Мебиуса с тремя полуоборотами, что является еще одной конструкцией [2].
Фабрис Гийо: в результате некоторых усилий воображения получается, что так же, как в результате разреза на
Поразительно, что в июльском примечании 1966 года, известном как топологическое дополнение к статье «О вопросе, предваряющем любое возможное лечение психоза», Лакан не указывает число полуоборотов, характеризующих ленту Мебиуса, то есть разрез miMI на схеме R, и также не уточняет, какой разновидностью проективной плоскости является схема R. Также, если это кросс-кап, который Лакан предпочитал использовать в качестве представления проективной плоскости в R3 на своих семинарах, то, без серьезных теоретических трудностей, становится возможным рассмотреть преобразование схемы R в поверхность Боя; чертежи, иллюстрирующие это преобразование еще предстоит создать. Более того, поскольку больше нет лишней куспидальной точки, использование поверхности Боя в качестве разновидности погружения проективной плоскости усиливает гомогенность [renforce l’homogénéité] структуры между лакановской формализацией фундаментального фантазма и математической формализацией поверхности: фаллос можно соотнести с полюсом, двусторонний диск — с объектом маленькое а, а ленту Мебиуса с тремя полуоборотами — с субъектом, возникающим в результате разворачивания означающей пары.
Наконец, если поверхность Боя оказывается подходящей для представления структуры фундаментального фантазма, вопрос о психоаналитическом смысле, который должен быть придан кросс-капу, появляется вновь и, следовательно, остается открытым. С этой целью и в качестве начала ответа мы можем найти на сайте Жан-Пьера Пети статью, описывающую этапы превращения кросс-капа в поверхность Боя с помощью малоизвестной топологической поверхности: Римской поверхности Штайнера, представленной на рисунке 12 ниже (разновидности погружения [immersion] промежуточной проективной плоскости, промежуточной между
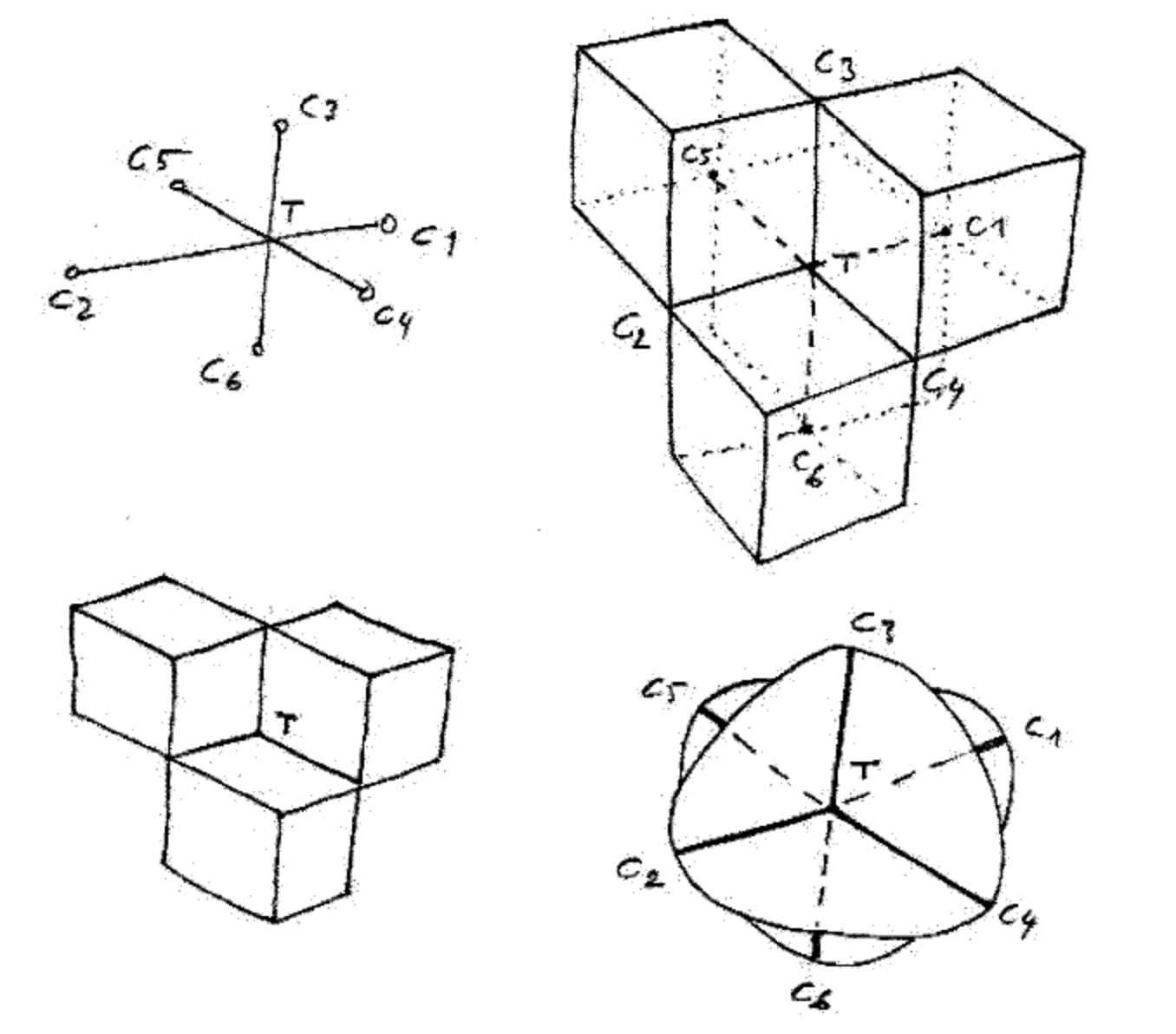
Жан-Пьер Пети: к концу дня мы, кажется, поставили фундаментальный фантазм на новые основания. Обрадованный, он решил пригласить меня к себе на ужин. Так я познакомился с его женой, которая очень тепло приняла меня.
Лакан, со своей стороны, был погружен в чтение «курса», который я читал в то время своим студентам-философам филологического факультета в
— Но почему вы размещаете эти картинки именно так?
— В противном случае вы не сможете листать этот документ.
Он улыбнулся.
— Вместо того чтобы ежегодно обучать двадцать студентов вашего факультета, вы не задумывались о том, чтобы охватить более широкую аудиторию?
— Как?
— Писать книги. Завтра я направлю вас к редактору, которому вас порекомендую.
Из этого диалога возникла коллекция альбомов Ансельма Лантурлу, которые были изданы в течение двадцати пяти лет издательством Belin. Увы, это издание только что закончилось, и Топологикон, который содержит описания, связанные с
Фабрис Гийо: в некотором смысле именно благодаря импульсу Лакана вы придумали и написали восемнадцать приключений вашего персонажа Ансельма Лантурлу по основным дисциплинам научного знания.
Жан-Пьер Пети: На самом деле это был не тот издатель, к которому Лакан направил меня (le Seuil). Серия комиксов вышла в издании Belin еще в 1979 году не без сложностей. Мне не составило труда создать первые три альбома, в том числе Геометрикон. Все это полностью поглотило меня в последующие месяцы, и после этого я больше не общался с Лаканом.
Я хочу рассказать смешную историю, которая произошла при издании этой серии комиксов. После нескольких месяцев проволочек руководство издательства Belin все еще не решалось. Генеральный директор постоянно спрашивал: «Это для детей какого возраста?». В то время я ездил в англоязычный Уорикский университет на семинар по просьбе моего друга — математика Кристофера Зимана. Эти комиксы приводили его в восторг. Когда я сказал ему о том, что застопорился на несколько месяцев, он ответил:
— Подожди. Скоро ты отправишься в Штаты. Я напишу издательству Belin и спрошу, будет ли им интересно, если я свяжусь с американскими издателями во время твоего пребывания в Штатах.
— У тебя есть контакты ?
— Ни одного, но, возможно, это даст пинок под зад.
Уловка сработала. Жан Оливецци, еще работавший в этом издательстве, очень помог мне своими советами в разработке нового и странного продукта «научный комикс». Он был поклонником комиксов. Войдя в курс дела, он подлил масла в огонь:
— Если мы пропустим эту серию, Пети подпишет контракт с американцами !
Французский Генеральный директор [в этой ситуации будто бы] стоял на вышке для прыжков в воду, в плавательной шапочке и ластах. И он прыгнул.
Фабрис Гийо: Но вы не просто иллюстратор совместной статьи с Бернардом Мораном о выворачивании сферы. Кроме этого у Вас было несколько важных находок, особенно в том, что касается поверхности Боя.
Жан-Пьер Пети: Возвращаясь к этой области геометрии, я хочу рассказать несколько довольно удивительных историй. В самом начале этого века (по-моему, это было в 1902 году) молодой студент по имени Вернер Бой придумал этот объект [поверхность Боя] и рассказал о нем своему учителю, знаменитому математику Гильберту. Тот нашел эту идею интересной и предложил своему ученику продолжить разговор после приближающихся каникул. Наступила осень, и Гильберт удивился, не увидев молодого Боя. Через некоторое время он отправился к нему домой в город, и его домработница ответила ему :
— Он уехал.
— Но он [наверняка] оставил адрес, по которому можно было бы с ним связаться.
— Нет.
И больше никто не слышал о Вернере Бойе. Мы так и не нашли его следов, и никто не знает, где он похоронен.
В конце 1960-х годов американский математик Смейл предсказал, что сфера может быть вывернута recto verso. Француз Бернар Моран, будучи слепым с пятилетнего возраста, придумал версию, ориентированную на модель, которая носит его имя. Затем один американский меценат предложил крупную сумму — миллион долларов — тому, кто мог бы построить соответствующие модели. Математик из Беркли Чарльз Пью сумел сделать их с помощью решетки для курицы-гриль. Эти модели годами украшали потолок кафетерия математического факультета Университета Беркли до тех пор, пока однажды ночью они не были… украдены. Никто не знал, кто их украл, мы их так и не нашли.
Пришлось ждать конца 1980-х годов, когда парижский Дворец открытий представил в «зале Пи» модель из металлической проволоки, которую я разработал, и которую скульптор Макс Соуз воплотил в жизнь. Эта модель экспонировалась более двадцати лет, но только что была снята и теперь находится в запасниках музея.
На рубеже 70-80-х годов я вместе с сыном математика Жана-Мари Сурио по имени Жером нашел первые уравнения, позволяющие получить синтетические изображения этого странного объекта. Я понимал, что поверхность можно описать с помощью семейства эллипсов (меридиановых линий), пересекающихся в одной точке — полюсе поверхности. Это позволило математику Апери построить первое так называемое «неявное» уравнение поверхности, очень сложное и тяжеловесное, но имеющее достоинство существовать и топологически описывать эту поверхность. Довольно неверно Моран приписал это открытие эллиптических меридианов скульптору Максу Соузу. Великие люди склонны мелочиться.
Я начал строить и продавать многогранные изображения поверхности Боя, которые были выставлены в книжном магазине в
Фабрис Гийо: Спасибо, в любом случае спасибо очевидцу за его ценное свидетельство, и спасибо астрофизику за его неопубликованное топологическое учение.
Библиография
MORIN, B. ; PETIT, J.-P. 1979. « Le retournement de la sphère », Pour la Science n° 15, p. 34-41.
LACAN, J. Le Séminaire Livre IX : L’identification, 1961-1962, inédit, Leçons du 28 mars et du 16 mai 1962. LACAN, J. 1966. « D’une question préliminaire à tout traitement possible de la psychose », dans Écrits,
Paris, Le Seuil, p. 553-554.
Резюме
Соглашаясь сообщить нам историю своих трех встреч с Жаком Лаканом, Жан-Пьер Пети делает гораздо больше, чем завершает параграф, оставшийся в тени столетней истории психоанализа во Франции. Он учит нас, что один топологический объект, поверхность Боя, привлек внимание Лакана до такой степени, что логически подразумевал перестройки в его более ранних топологических формулировках, которые никогда не предпринимались при его жизни. Существование сингулярности кросс-капа, остававшееся незамеченным, доказательство существования такой сингулярности, подробное описание поверхности Боя и преобразования, произведенные нанесением разреза на такой объект — это три пункта, которые он показал Лакану и которые согласился снова представить нам вместе с собственноручно сделанными топологическими записями.
[1] Научно-образовательный комикс на тему топологии.
[2] Подробнее об этих трансформациях можно прочитать в тексте Фабриса Гийо «Топологизация схемы R Жака Лакана в поверхность Боя»
[3] Эти работы можно найти на сайте Жан-Пьера Пети.
