Субъект бессознательного и шов
Если вы начнете читать семинар «Важнейшие проблемы психоанализа», то очень скоро столкнетесь с понятием «шов». Прочитав чуть дальше, вы обнаружите, что с ним связаны некоторые сложности. Речь идет о том, что в ходе этого семинара Лакан предлагает проводить так называемые «закрытые встречи». Это встречи, на которых будет говорить не он, а участники семинара. Именно поэтому о шве будет говорить не только Лакан, но и Миллер с Леклером. Все они используют это слово, но если чуть приглядеться, то можно увидеть, что речь идет о разных швах. Этим текстом мы хотим внести ясность в различие между этими швами, что позволит потенциальному читателю лакановских семинаров испытать при чтении чуть меньше трудностей, чем пришлось это сделать нам.

Часть 1: Шов и субъект
В начале своего семинара Лакан задается вопросом: почему каждый раз, когда мы пытаемся сказать, что такое Означающее, остается какая-то неясность, непрозрачность? Это не только вопрос «стиля» Лакана, — куда больше это связано с самим языком. Каждый раз, когда язык пытается сказать о самом себе, он терпит неудачу, происходит какая-то потеря. Здесь Лакан вполне согласен с Витгентштейном времени «Логико-философского трактата». Для Витгентштейна язык прекрасно приспособлен, чтобы описывать реальность, но он не может сказать о своем собственном устройстве.
Означающее — не линия
В качестве некоторого выхода из этой невозможности Лакан предлагает обратиться к топологии, без которой в вопросе структуры языка не обойтись [1].
И первое его предложение — это перестать мыслить означающее как линию (как предлагает это делать Соссюр).
«Означающее, являясь по своей природе воспринимаемым на слух, развертывается только во времени и характеризуется заимствованными у времени признаками: а) оно обладает протяженностью и б) эта протяженность имеет одно измерение — это линия».
По словам Лакана, этого недостаточно: нам необходимо найти что-то другое.
Он говорит о сети означающих, а любая сеть может быть сведена к поверхности. Почему же речь идет о сети? Всем нам знакомо понятие «цепочка означающих», но и тут и в 11 семинаре Лакан говорит именно о сети. Сеть предлагает нам уже не одно, а два измерения: синхрония и диахрония. В каждый момент времени из многообразия означающих субъект выбирает одно, что в диахронии дает эффект предпочтения, т.е. из сети выбирается цепочка. Мы действительно имеем дело с цепочкой, но только в том случае, если забываем об измерении синхронии, возможности субституции.
Эти два измерения описаны уже Соссюром; тем не менее, он придерживается традиционного убеждения о сугубо линейном характере языка. Кажется, что этот переход от линии к поверхности Лакан совершает благодаря Якобсону, который настаивает не на линейности языка, но на присутствии в нем двух различных измерений. С одной стороны это отношения смежности (комбинации), а с другой — селекции. Таким образом, перед нами уже не линейная структура, но поверхность или сеть.
Следующим шагом Лакан уточняет, о какой именно поверхности идет речь.
Вместо линии Лакан предлагает мыслить означающее как ленту Мёбиуса, поясняя этот момент следующим образом. И на той и на другой стороне мы встречаем фонематический материал; таким образом, становится ясно, что обе стороны не что иное, как одна. «Материал, который структурирован здесь из фонематической оппозиции, является тем, что не переводится, а проходит, переходит от одного знака к другому».
Этот тезис — вероятно, один из основополагающих для всей лакановской топологии. Конечно, он заслуживает куда более подробного комментария, но сейчас нам придется оставить его в подвешенном положении, поскольку то краткое пояснение, которое он дает, кажется пока более чем туманным. Таким образом, мы, вслед за Лаканом, вводим его сейчас скорее в догматическом ключе, и обязательно обратимся к нему в следующих текстах.
Тем не менее, это замечание позволяет нам перейти к следующим размышлениям Лакана.
Космоса не существует, или картезианский «переворот»
Эта одна из самых известных фраз о несуществовании стала таковой не столько благодаря семинарам Лакана, сколько его встрече с Алексеем Леонтьевым, которую организовал Рене Заззо.
Дело в том, что, по словам Заззо, Лакан хотел поехать в СССР, — причем в качестве не туриста, а приглашенного, и на относительно длительный срок (несколько месяцев). Это желание возникло у Лакана в связи с нашумевшим подвигом Гагарина.
«Я очень хочу поехать в СССР. Мне нужно многое им [советским людям] сказать. Нужно все пересмотреть. Сейчас, когда человек проникает в космическое пространство (espace), возникает новая психология (une nouvelle psychologie)».
Он хотел познакомить жителей Советского Союза с настоящим психоанализом, организовать семинар. Лакан попросил Заззо посодействовать ему в этом и тот договорился с Леонтьевым о встрече в одну из поездок советского психолога в Париж.
Некоторое время спустя эта встреча состоялась. Главными ее действующими лицами были Лакан, Леонтьев и Заззо. Довольно долго Лакан и Леонтьев не разговаривали. В
Эта фраза осталось непонятой не только присутствующими, но и многими из тех, кто Лаканом интересуется, изучает его семинары. Обычно ее интерпретация сводится примерно к следующему: «Слово “космос» устарело. Мы не говорим больше о гармонии, вечном порядке, небесных сферах, — мы имеем дело с другим Космосом”. Все это конечно верно, но неполно. Говорить так, значит говорить примерно следующее «Зигмунд Фрейд причастен к идее Эдипового комплекса».
Давайте попробуем разобраться, о чем же
«Космос» для Лакана — не только некоторое представление о гармонии небесных сфер, но еще и определенная структура, характерная для самого языка в определенный период. Эта структура отражения — отражения микрокосма в макрокосме.
Иными словами, «Космос» отсылает не столько к некоторому объективному устройству Вселенной, сколько к языку. Лакан скажет, что «язык входит в реальность и создает там структуру».
Мы предполагаем, что, говоря об этой идее языка как отражения макрокосма и микрокосма, об этом взаимном подобии, Лакан ссылается на Фуко.
В своей работе «Слова и вещи» Фуко описывает устройство трех различных эпистем, первая из которых сильно напоминает то, о чем говорит Лакан:
«Вплоть до конца XVI столетия категория сходства играла конструктивную роль в знании в рамках западной культуры […]
Мир замыкался на себе самом: земля повторяла небо, лица отражались в звездах, а трава скрывала в своих стеблях полезные для человека тайны.»
Фуко говорит о четырех формах подобия: пригнанность, соперничество, аналогия и симпатия/антипатия.
Согласно его теории, до появления классической эпистемы знак имел троичную форму. Он включал в себя два объекта и примету. Примета, не являясь частью этих объектов, конституирует их подобие.
«Между волчьим корнем и глазами существует симпатия. Если бы на растении не было приметы, отметины и как бы слова, сообщающего, что это растение благотворно для больных глаз, то это непредвидимое сродство оставалось бы скрытым. Такой знак легко прочитывается в его семенах: это маленькие темные шарики, помещенные в белые оболочки, представляющие примерно то же самое, что и веки для глаз. То же самое и относительно сродства между орехом и головой: толстая зеленая корка, охватывающая кость — раковину — плода, лечит раны надкостницы черепа, однако внутренние боли головы предотвращаются самим ядром ореха, в совершенстве демонстрирующим мозг.»
Кроме того, Фуко также настаивает на фундаментальной важности идеи соответствия микрокосма и макрокосма:
«Именно здесь вступает в дело пресловутая категория микрокосма. Пожалуй, именно благодаря известной традиции неоплатонизма это старое понятие сохраняло свою жизнеспособность в течение средневековья и раннего Возрождения. Но в XVI веке оно в конечном счете стало играть основополагающую роль в знании […]
В качестве категории мышления оно применяет ко всем сферам природы игру повторяемых сходств; гарантирует исследованию, что каждая вещь найдет при более широком охвате свое зеркало и свое макрокосмическое подтверждение».

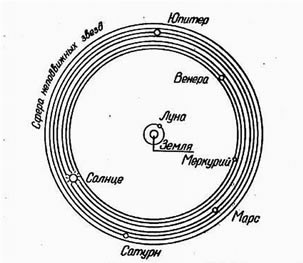
Таким образом, язык функционировал по принципу подобия, отражения. Именно это интересует Лакана, и в этом отправная точка его мысли. Такую структуру, где одно отражается в другом и одновременно его содержит, обычно изображают в виде нескольких концентрических сфер. Рисунки 1 и 2 отображают представления греков о космосе.[2]
В ходе семинара Лакан берется показать, какие изменения произошли с этим сферическим миром подобий благодаря возникновению субъекта.
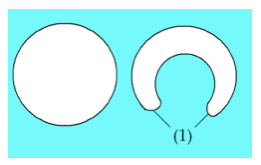
Для начала он берет сферу и начинает ее деформировать (рис 3). В результате такой деформации сфера уже напоминает не шар, а скорее ручку гири. Такое преобразование в топологии является допустимым, поскольку не меняет структуру поверхности.
Далее Лакан продолжает растягивать нашу сферу, получая тем самым как бы две сферы (1 и 2), но которые на самом деле являются лишь частями одной и той же (рис 4).
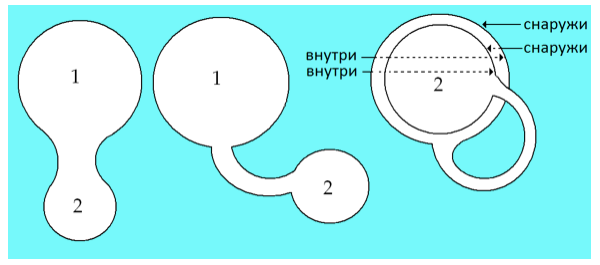
Последнее преобразование состоит в том, чтобы поместить одну из этих частей в другую. Чтобы произвести эту операцию, нам нужно, чтобы сфера сама себя пересекла.Несмотря на то, что Лакан никак не поясняет этот момент, мы могли бы прокомментировать, что здесь идет речь о свойствах не объекта (идея как раз в том, чтобы сфера сохранила все свои свойства), а репрезентации.
Так, в топологии различают свойства, присущие объекту самому по себе, и свойства, связанные с его погружением в пространство. Самопересечение, о котором идет речь, относится ко второму типу свойств, т.е. является эффектом погружения нашей сферы в трёхмерное пространство.
Эта структура сферична, и мы получили такую репрезентацию путем непрерывных преобразований, без выполнения разрезов и склеиваний.
Итак, у нас есть одна сфера, которая одновременно является и внешней и внутренней — макрокосмом и микрокосмом, где обеспечивается бесконечная игра отражений и подобий.
Однако в определенный момент структура меняется. Этот момент ознаменован появлением картезианского cogito, которое и разрушает космос, создавая на его месте что-то принципиально иное.
"Я уже раньше позволил себе высказать убеждение, что область, на которую направлены изыскания Фрейда, не могла быть открыта иначе, как по прошествии некоторого времени после появления картезианского субъекта, ибо вся современная наука вообще возникла лишь после того, как Декарт сделал свой решающий, основоположный для нее шаг. Благодаря этому шагу, и только ему, можем мы теперь позвать субъекта в Бессознательное — туда, где он находится у себя дома. Ведь, чтобы позвать кого-то, нужно, по крайней мере, знать, кого мы зовем. Ведь зовем-то мы не старую знакомую нашу, бессмертную — или смертную — душу, не тень, не призрак, не
Чтобы понять концепцию Фрейда, необходимо исходить из того, что призванным является у него именно субъект — субъект картезианского происхождения.»[3]
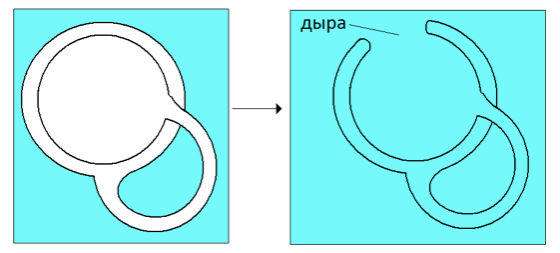
Появление субъекта меняет структуру языка. Для Фуко это момент перехода от троичной структуры знака к двоичной (означающее/означаемое) — к представлению.
Что же представляет собой этот субъект и как он меняет сферическую структуру?
Появление субъекта является ни чем иным, как появлением дыры. Это неудивительно, если мы помним, что Лакан определяет субъекта как нехватку.
Однако эта дыра устроена немного хитрее, чем дыра на обычной сфере. Вероятно, именно для того, чтобы показать специфику этой дыры или же внести различие между дырами, Лакан и прибегает к топологии. То есть, ему недостаточно сказать, что субъект это дыра или нехватка: важно указать именно на различие дыр, поскольку та дыра субъекта, о которой он говорит не носит интуитивный характер.
Еще раз попытаемся отметить специфику операции, в которой возникает дыра субъекта. Здесь имеют место два действия:
1) Мы проделываем дыры в «маленькой» и «большой» сферах.
2) Сшиваем их края.
В этот момент мы создаем Шов (Лакан также называет это место «точкой пристежки»), и назначение этого шва — открывать дыру. Таким образом, как мы увидим дальше, речь идет о достаточно специфическом шве, который не зашивает дыру, а ее образует, что полностью противоположно природе швов, о которых мы будем говорить дальше.
Нетрудно заметить, что появление дыры, проделанной таким образом, преобразует сферу в бутылку Клейна. Она представляет собой одностороннюю поверхность без края, внутренняя часть которой сообщается со внешней.
Но почему же появление субъекта дестабилизиует прежнее функционирование знака как троичного? Прежде всего потому, что субъект не укладывается в его структуру. Картезианский субъект — это более не человек и не душа: это субъект познания, мыслящая вещь, трансцендентная миру, который этот субъект изучает. Однако он представлен означающим, о чем нам говорит излюбленная лакановская формула.
Таким образом, мы могли бы сказать, что субъект не только эффект означающего, но и то, что означающее — эффект субъекта, в том смысле, что начиная именно с этого момента означающее выступает в своей истинной функции: «представлять субъект перед другим означающим» [4].
Лакан настаивает, что именно появление этого субъекта открывает путь современной науке, парадигмой которой является математизированная физика — наука, которая ответственна за запуск человека в космос. За тем лишь исключением, что речь уже идет не о космосе, а
Гагарин — не космонавт, поскольку сам факт его путешествия в космосе, пройденной им траектории — нечто непредвиденное, если мы рассматриваем космос как гармонию сфер. В таком космосе ему просто нет места, поскольку этот полет тут же всю гармонию нарушает. То место, где побывал Гагарин, Лакан скорее назвал бы а-космосом, то есть пространством, которое подразумевает принципиальное другое пользование языком.
Необходимую траекторию, согласно законам гравитации, удалось найти только исходя из отказа от всех космических очевидностей.
Говоря о космосе, Лакан, конечно, прежде всего имеет в виду структуру языка. «Входя в реальность, язык создает там структуру, для описания которой нам потребуется прибегнуть к топологии».
Часть 2: Шов Миллера
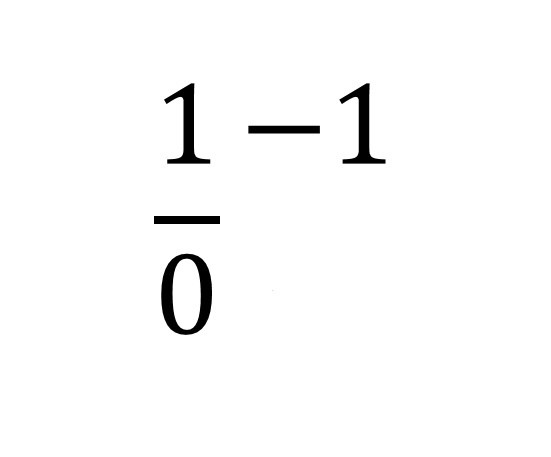
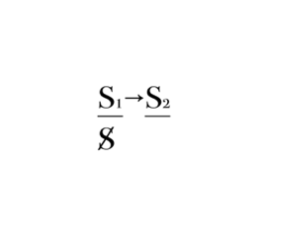
На одном из занятий Лакан скажет, что способ, которым мы записываем нашу формулировку означающего, имеет непосредственное отношение к математике. Так же, как означающее представляет субъект для другого означающего, так и единицы представляют ноль для других единиц.
Речь идет о программе логицизма Фреге. Занимаясь вопросами обоснований оснований математики, Фреге предлагает свести математические операции к логическим, исключив при этом психологизм. Фреге хочет логически обосновать арифметику, то есть не ссылаться на «мыслящего субъекта», результатом работы душевных процессов которого и будет возникновение числа. Иными словами, этот подход не требует наличия субъекта, который считает овец, камни или что-то еще. Арифметика в этом подходе сведена исключительно к логическим понятиям и существует независимо от субъекта.
Комментированию и интерпретации этого высказывания Лакана будет посвящено несколько закрытых семинаров, на которых разгорится нешуточный спор между Сержем Леклером и
Доклад Миллера, как и написанная по его мотивам статья[5], посвящен интересующему нас понятию шва. В самом начале своего текста Миллер дает шву определение:
«Шов — это элемент, обеспечивающий связь субъекта с цепочкой его же дискурса», или «Шов — это связь нехватки со структурой».
Попробуем прояснить эти определения, но перед этим отметим, что основная мысль Миллера заключается в том, что субъект в ряду натуральных чисел, о которых говорит Фреге,
Основные моменты, к которым он уделяет внимание, комментируя работу Фреге, — это определения 0, 1 и понятие следования.
Число
В своей работе Фреге последовательно рассматривает существующие подходы к пониманию числа и, выявляя их неудовлетворительность, приходит к тому, что число имеет отношение не к объектам, но к понятиям:
«Если при рассмотрении одного и того же внешнего явления я с одинаковой истинностью могу сказать: “Это — группа деревьев» и «Это — пять деревьев» или «Здесь находится четыре группы людей» и «Здесь находится 500 человек”, то при этом изменяется не отдельное и не целое, не агломерат, а моё название. Но последнее есть лишь знак замены одного понятия другим. Вследствие этого, как ответ на первый вопрос предыдущего параграфа нам больше подходит то, что указание на число содержит высказывание о понятии.»
То есть, обращаясь к объектам мира самим по себе, мы не можем присвоить им число. Чтобы эта операция стала возможной, необходимо ввести понятие, — только в соответсвии с ним и возможен счет.
Иначе говоря, число — это объем понятия.
Мы могли бы предложить следующую схему, которая делает очевидным, что подобный подход предполагает 3 уровня:
Понятие — число
|
Объекты
Если мы возьмем понятие «естественный спутник Марса», под него подпадает 2 объекта: Фобос и Деймос. Следовательно, понятию «естественный спутник Марса» присваивается число 2. Еще раз обратим внимание, что единицей здесь является не объект Фобос или Деймос, а «естественный спутник Марса».
«естественный спутник Марса» — 2
|
Фобос, Деймос
Для Фреге этот момент важен еще и тем, что речь не идет о том, что объекты являются равными. Фобос и Деймос различны; равными являются единицы которые к ним относятся, поскольку и один и второй подпадают под понятие «естественный спутник Марса». Тот факт, что число относится к понятию, а не к объекту, позволяет нам предположить различие этих объектов в реальности.
Но Фреге не останавливается на указании того факта, что число имеет отношение к понятию. Формулировка, к которой он придет, будет следующей:
«Итак, я определяю: число, соответствующее понятию F, есть объём понятия «равночисленно понятию F».
Чтобы пояснить о чем идет речь, нам придется обратиться к понятию равночисленности. Фреге задается следующим вопросом: «Каким образом мы можем узнать, что два числа равны? Как нам определить, что n=m?»
В качестве ответа он предлагает процедуру биекции. Биекция представляет собой операцию, когда в соответствие каждому элементу одного множества мы ставим один и только один элемент другого множества.
Фреге приводил следующий пример:
«Если официант хочет быть уверен, что он положил на стол ножей столько же, сколько тарелок, ему нет надобности считать каждый из них; если только он справа от каждой тарелки рядом положил нож, тогда каждый нож на столе находится рядом справа от тарелки».
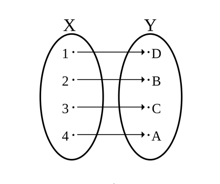
Объем множества «тарелки» равен объему множества «ножи», каждому элементу первого множества соответсвует один и только один элемент второго, и наоборот.
Тогда, чтобы ответить на вопрос «Сколько здесь ножей?», мы можем не пересчитывать ножи так же, как мы пересчитывали спутники. Достаточно просто ответить: «Столько же, сколько и тарелок».
Эта идея равночисленности говорит нам следующее: число 4 (и любое другое) теперь не закреплено только за понятием «сторона света» — оно соответствует всем понятиям с объемом, равным объему понятия «сторона света». Например: углы квадрата, «количество букв в слове “стол»”, «конечность собаки».
В своем тексте Миллер использует слово «identique», которое в русском переводе вместо «равночисленного» превратилось в «идентичный». Мы всё же думаем, что речь идет о равночисленности, — иначе представляется весьма проблематичным понять то, что имеет ввиду Миллер.
По его версии, в операции подпадения объекта под понятие и присвоения ему числа происходит то, что он называет «стиранием вещи» и «рождением логического измерения». Иными словами, переход из мира объектов в поле логики. Однако его пример всё же выглядит немного иначе, поскольку то, о чем он говорит — это удвоение понятия То есть, Миллер не берет равночисленное понятие, как, например, «глаза Сократа» или «руки Платона», а удваивает существующее.
Так, в его примере с понятием «ребенок Агамемнона и Кассандры», под которое подпадают Пелопс и Телегам, чтобы получить из них единицы, он предлагает «применить их к самим себе». То есть, поставить элементы множества «ребенок Агамемнона и Кассандры» в однозначное соответствие к самим себе. Для него это единственно возможный способ появления числа:
«Этому набору я смогу поставить в соответствие число, только опираясь на следующее понятие: «идентичный понятию “ребенок Агамемнона и Кассандры»”. Таким образом, посредством этого удвоения понятия, по мнению Миллера, производится переход от вещи (и ее одновременного «стирания») к единице, то есть переход от реальности к логике.
Зачем Миллер производит это удвоение, не слишком понятно. На вопрос «Сколько женщин в этой комнате?» вполне можно ответить: «Столько же, сколько у тебя пальцев на обеих руках». Но вот ответ «Столько же, сколько здесь женщин» является тавтологичным. Безусловно, это верный ответ, поскольку он опирается на закон тождества [6], но благодаря ему мы так ничего и не узнали. В связи с этим то, как понимает равночисленность Фреге, нам кажется более удобным.
Ноль и единица
Выше мы увидели, как Фреге и вслед за ним Миллер показывают, что число имеет отношение к понятию, а не к объектам мира. Мы могли бы сказать, что реальность «нарезается» посредствам понятия.
Однако, когда Фреге подходит к определению 0, 1 и операции следования, он делает это аксиоматически, то есть, больше не обращается к объектам мира, а задает числа аксиомами, — так же, как это происходит в геометрии Евклида. В этом и будет состоять суть программы логицизма.
Фреге начинает с определения нуля.
Ноль он определяет как число, которое соответствует понятию «не равное себе». Он выбирает такое понятие, чтобы избежать любой ссылки на эмпирику и остаться в измерении логики; в этом и состоит его основная идея.
«Я могу принять за определение 0 любое другое понятие, под которое ничего не подпадает. Но дело в том, что мне нужно выбрать такое понятие, которое может быть доказано чисто логически; и для этого «не равное себе» представляется удобным.» Cуждение ‘а ≠ а’ является априорно ложным, постольку необходимо истинно то, что не существует не равных себе предметов. Следовательно, под понятие ‘не равное себе‘ не подпадает ни один предмет.
«Не равен себе» — 0
|
—
Понятие «быть равным» Фреге заимствует у Лейбница. Оно звучит следующим образом: «Тождественные суть те, один из которых может быть поставлен вместо другого с сохранением истинности».
Попробуем перефразировать, чтобы стало ясно, о чем идет речь:
«Два выражения считаются одинаковыми, если одно из них всегда может быть подставлено вместо другого, причем истинность целого не изменяется».
Иными словами, в равенстве 2+2=4 мы можем заменить правую часть на 3+1 (поскольку 4=3+1) и получим 2+2=3+1. Равенство осталось верным, мы не потеряли в истине.
Кажется, что дело обстоит еще проще, если мы заменим объект им самим, т.е. в нашем примере мы заменим 4 на 4. Поскольку четверка тождественна сама себе, то равенство также сохраняет свою истинность.
Иначе говоря, равенство вещей самим себе является в данной модели гарантом истины. И наоборот: если вдруг появляется вещь, которая не равна себе, то это разрушает истину. В логике, которую предлагает Фреге, объекту, не идентичному самому себе, не находится места.
И именно здесь Миллер указывает на шов дискурса в логике. Этот шов располагается на месте исключения неидентичности самому себе. Психоанализ не может руководствоваться той логикой, о которой говорит Фреге, поскольку имеет дело с этой неидентичностью. Достаточно вспомнить известные шутки про зонтики и бананы, чтобы сказать, что в опыте, с которым сталкиваются аналитики и анализанты, измерение неидентичности явно присутствует. Понятие бессознательного охватывает вещи, не тождественные самим себе. В качестве примера мы можем вспомнить известную эквивалентность, которую предлагает Фрейд: кал/деньги, ребенок/пенис.
Таким образом, логика — это то, что основано на законе тождества А=А, тогда как в анализе это равенство является ложным. Мы могли бы подумать, что именно об этом говорит Миллер, но, как мы увидим дальше, это не так: для него эта неидентичность связана не с означающим, но с субъектом.
Он заявляет, что речь для нас идет о построении этой логики неидентичности, необходимой для психоанализа.
Аналитик не может руководствоваться логикой логиков, — ему требуется что-то иное, что Миллер называет логикой означающего, наброски которой он и предлагает. Эта логика должна дать нам возможность учитывать измерение несамотождественного.
Далее определим единицу.
Для этого возьмём понятие «равный нулю» (мы берем именно 0, а не любое другое число, поскольку ноль — единственное число, которое было нами определено). Или мы можем записать так: «равен не равному себе». Под такое понятие подпадает лишь один объект — это ноль. Следовательно, понятию «равный нулю» соответствует число 1, или объем понятия «равен нулю» равен единице. Стоит обратить внимание на то, что, когда мы определяли ноль, он был задействован на уровне понятия, тогда как сейчас он задействован на уровне объекта, подпадающего под понятие.
«Равен 0» — 1
|
0
Понятие следования
Далее мы обратимся к понятию следования, и именно здесь сможем увидеть появление формулировки, предложенной Лаканом.
Что такое понятие следования? Это вопрос того, каким образом нам задать число n+1, то есть следующее за n число.
Миллер, вслед за Фреге, определяет это достаточно просто: число n+1 соответствует понятию «натуральный ряд чисел, заканчивающийся на n». Этот момент может немного смутить, но давайте посмотрим внимательнее. Возьмем в качестве примера «натуральный ряд заканчивающийся на 3». Нам требуется определить количество элементов, которые соответствуют этому понятию: 1, 2, 3…и 0[7]. Именно поэтому числом, которое мы присвоим нашему понятию, будет 4, тогда как сам этот ряд заканчивается тройкой.
Это происходит благодаря тому, что ноль (как и все остальные числа этого ряда) считается за единицу.
То, что было ничем на уровне реальности и нулем на уровне понятия, посчитано за единицу.
Мы обращаем внимание читателя, что все это возможно благодаря тому, что ноль занимает различные позиции в каждой из этих операций. Когда мы говорили о понятии «неравный себе», ноль был числом, соответствующим этому понятию. Сейчас же, когда мы говорим о понятии «натуральный ряд, заканчивающийся на 3», ноль уже находится на уровне объекта.
«натуральный ряд чисел, заканчивающийся на 3» — 4
|
0,1,2,3
Но как все это относится к психоанализу и его субъекту? Лакан уже приводил в качестве примера эксперимент Пиаже, когда мальчик, у которого два брата, отвечал на вопрос «Сколько у тебя братьев?» — «Три».
Здесь же Лакан приводит другой пример. Речь идет о девочке 4,5 лет. Перед ней стоят 3 стакана, и, сидя перед ними, она уверенно говорит: четыре!
«Четвертый — это ее 0, поскольку от него она начинает считать, поскольку в свои 4,5 она уже маленький круг, дыра субъекта.»
В обоих этих примерах субъект появляется на двух уровнях: как тот, кто ведет подсчет, и как тот, кто подсчитывается. Обычно говорят, что эти дети совершили ошибку, или подсчитали что-то лишнее, но Лакану удалось заметить, что «лишнее» — это субъект. Также как в случае нашего ряда, заканчивающегося на 3, в котором неожиданно возникал 0, так и в случае этой девочки возникает субъект. Иными словами, в этой оговорке субъект возникает в качестве единицы. Лакан обращает внимание на то, что в поле речи этот ноль, эта дыра субъекта возникает в качестве единицы.
«Отношения нуля и единицы не что иное, как матрица отношений субъекта к полю Другого.»
Излишек, которым является ноль в операции следования, показывает нам, каким образом субъект запускает цепочку означающих. Именно таким образом мы могли понять невозможность субъекта совпасть с ней, поскольку сказанное тотчас подразумевает еще одно (+1), которое представляет субъекта в поле Другого и так без конца.
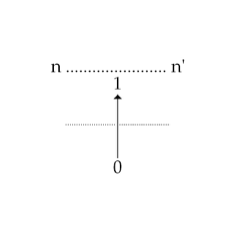
Комментируя эту операцию следования, Миллер предлагает перейти от ее классической горизонтальной репрезентации: n… n+1… n’ к вертикальной (рис 9).
Мы попытаемся продемонстрировать достоинства этой записи. Если в понятии следования «n + 1» единицей является эффект подсчета нуля, то знак "+" указывает на пересечение черты поля истины (переходом в поле истины Миллер называет переход от реальности к понятию, поскольку последнее имеет логическую природу), в котором ноль и появится в качестве единицы. Этот эффект пересечения черты, в котором вместо одного появляется другое, напрямую связан с функцией метафоры.
Таким образом, перед нами переход от того, что мы могли бы назвать полем объектов (поскольку ноль берется именно именно в этом качестве, то есть как объект, подпадающий под понятие «натуральный ряд чисел, заканчивающийся на n») к полю истины, где они появляются в качестве единиц.
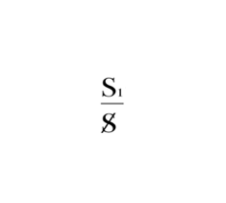
В этой вертикальной репрезентации уже угадывается знакомая всем вертикальная запись отношений субъекта и означающего.
Однако Миллер вслед за Лаканом настаивает, что речь идет не просто об аналогии, но о строгом структурном соответсвии, и структура, о которой идет речь, называется «шов». Так же, как субъект появляется в поле Другого только через означающее, так и ноль появляется в поле истины в качестве единицы [8]. И один и второй репрезентированы в поле истины чем-то другим, что коррелятивно исключению их из этого поля. Субъект появляется в речи только через своего представителя.
Здесь мы хотели бы сделать некоторое пояснение. Миллер говорит о поле истины в двух ключах, которые совпадают. Первое — это поле логики, которое существует благодаря тому, что вещи идентичны сами себе. Тогда мы можем сказать, что в том мире, где это условие выполняется, — истина существует. Это и есть мир или поле истины. Сами объекты не могут там появится, как это было с числом 0; необходимо, чтобы он прошел процедуру попадания под понятие, чтобы стать объектом логическим. Когда наши объекты подпадают под понятия и тем самым понятиям атрибуируется число, тогда мы говорим о переходе в поле истины, в котором объекты уже функционируют через своих представителей.
С другой стороны, место истины это большой Другой, — именно так определяет это Лакан в ранних семинарах. Единственная возможность субъекту быть представленным на уровне Другого, это быть представленным через посредника, означающее, что имеет своим эффектом его исчезновение.
Еще раз отметим, что структура шва подразумевает два ключевых момента:
1. Первый — это шов логики, на который указывапет Миллер; тот, который исключает неидентичность самому себе и сохраняет истину.
2. Второй (тот, о котором мы только что сказали), — это то, как связаны ноль и единица, субъект и означающее.
Тем не менее, как кажется, Миллер в своем сообщении склеивает эти два уровня. Склейка, о которой идет речь, происходит в тот момент, когда он приравнивает 0 и неидентичность (хотя, конечно, 0=0), хотя изначально они располагались на разных уровнях, и ноль был числом, соответствующим понятию «неидентичность самому себе». Это стирание маркера позволяет ввести неидентичность в числовой ряд в качестве нуля, где она снова будет находиться вне поля истины, и куда может попасть только в качестве единицы. Именно поэтому он скажет, что здесь есть некоторая парадоксальность в том, что неидентичное представлено идентичным.
Миллер настаивает на этом свойстве противоречивости; для него субъект задается именно так. Тогда для как Фреге это просто удобный способ задать число 0.
Здесь мы должны были бы закончить, однако не можем не обратить внимания, что та логика неидентичности, о которой мы говорили выше, для Миллера выглядит совсем не так, как предполагали мы. Наша идея была в том, что неидентичным является означающее, на чем и настаивает Лакан в 9-м семинаре. Тогда как для Миллера представитель, т.е. означающее, идентично себе, а неидентичным, или противоречивым является субъект (отсюда и появляется фраза «неидентичное представлено идентичным»), что и является основанием для его исключения из поля истины. Кажется, что Миллер и Лакан говорят совершенно разные вещи. Лакан ничего не говорит про неравенство субъекта самому себе, но в ходе всего семинара «Идентификация» настаивает на том, что означающее это то, что не подчиняется закону тождества. Здесь мы можем кратко сказать, что там же он выделяет единичную черту, или единицу как суть означающего, — то, что и являет собой абсолютное различие. Иными словами, для Лакана подобное равенство 1=1 будет ложным, что кажется полностью вытеснено из речи Миллера, где единица предстает гарантом идентичности. Тем не менее, Лакан будет несколько раз ссылаться на этот его доклад, основная заслуга которого, как нам кажется, состоит в экспликации этой идеи отношений означающего и субъекта с опорой на Фреге.
Часть 3: Имя собственное
Здесь мы не будем подробно воспроизводить подход к имени собственному у Лакана [9], но лишь обозначим основные моменты. Обращаясь к позициям Гардинера и Рассела, он говорит, что ни одно из определений не может быть для нас удовлетворительно.
Для Рассела имя собственное — это обозначение вне дескрипции. У нас есть два способа обозначить вещь: первый — это ее описать, а второй — указать на ее особенности. Причем Рассел связывает этот второй способ с указательным местоимением «это» (this). Так, вы говорите «это — Петр», тем самым обозначая Петра вне описания: вы не говорите, высокий он или низкий, где он находится или чьим сыном является. Кроме того, у Рассела есть другой важный момент, а именно: такие имена, как Сократ, Гамлет и другие, не являются для него именами. Он скажет, что речь идет об описании. Когда вы говорите «Сократ», то речь идет именно о дискрипции «учитель Платона», или «человек, который выпил сок цикуты». Таким образом, перед нами краткие дескрипции. Подобный ход мысли кажется Лакану неудовлетворительным.
Гардинер же, в свою очередь, ставит акцент на звукоразличительной функции имени собственного. «Имя собственное — это слово (группа слов), осознаваемое как указывающее (или склонное указывать) на объект (объекты), с которыми оно соотносится исключительно посредством дистинктивного звучания, безотносительно любого значения, изначально присущего этому звуковому комплексу или приобретенного им через ассоциацию с указанным объектом или группой объектов».
Лакан удивляется, что лингвист мог дать такое определение имени собственному, тогда как звуковое различие — то свойство того материала, с которым он работает в первую очередь, — это свойство фонем.
Чтобы понять, как Лакан подходит к имени собственному, необходимо вспомнить то, что мы сказали о связи единицы и нуля. Их связь мы назвали «швом», и почти точно так же Лакан говорит об имени и субъекте. Если субъект представляет собой нехватку, дыру, то имя собственное — это то, что накладывает на нее шов. Но Лакан отмечает, что шов, о котором идет речь, — это шов ложный. Эта дыра не может быть зашита, но может создаться такая видимость. Благодаря этому ложному шву то, что является бутылкой Клейна, о которой мы говорили в самом начале, может быть принято за сферу, поскольку эффект сшивания (пусть даже и ложного) будет именно таким. То, что является нехваткой на одном уровне, предстает на уровне речи под именем собственным чем-то одним.
Кроме того, Лакан указывает, что подобный шов может быть наложен различными способами. Он рассказывает историю одного писателя, который делился своим опытом. Назвать литературного героя так или иначе — совершенно не всё равно. Этот процесс выбора имени очень важен, поскольку при удачном подборе он станет живее, чем живые люди. Иначе говоря, чтобы научиться писать, нужно поднатореть в искусстве накладывать швы. Другой пример рождается в обсуждении слова «космонавт». Лакан говорит, что это слово не слишком хорошо — по тем причинам, о которых мы говорили в 1-й части. Космоса не существует, а потому этих людей, космонавтов, мы могли бы называть иначе. Почему бы, говорит Лакан, нам не называть их, например, ангелами? В этот момент в зале раздается смех. Вот видите, — говорит он, — поэтому мы и не можем дать какое угодно имя новому явлению.
Конечно, когда мы говорим о единице или имени собственном, речь идет об идентификации; причем, на это нужно обратить внимание, — речь идет исключительно об идентификации с означающим. Идентификация — это то, что призвано заклеить нехватку, и именно поэтому Лакан рассматривает ее только как остановку на пути анализа.
Часть 4: Аналитик и шов
Мы уже сказали, что вокруг доклада Миллера разгорелся спор. В этом споре нас заинтересовало то, что в нем задействовано понятие шва, причем в несколько ином смысле, чем мы говорили об этом ранее.
Тезис Леклера состоит в том, что аналитик — это тот, кто «не сшивает», или, по-меньшей мере, кто должен воздерживаться от этой страсти.
Таким образом, «накладывать шов» — это действие, которое можно либо совершать, либо нет.
В этом пункте Миллер согласен со своим оппонентом. При этом он добавляет: то, что позволяет аналитику воздерживаться от «сшивания», — это его желание. Но что же имеется в виду под «сшитой» речью? В своем докладе Леклер поясняет это через идею места. Аналитик — это тот, кто не занимает определенного места, когда говорит; иными словами, это тот, у кого нет места. Далее Леклер добавит: «Тот день, когда аналитик окажется на своем месте, знаменует конец анализа».[10]
Отдельно от Леклера попробуем сформулировать свое понимание термина «сшитая речь». Мы могли бы сказать, что это речь, которая полностью исключает субъекта, — та, которая призвана заклеить все свои лакуны. Наложить шов — значит сделать свою речь убедительной (например, сославшись на авторитет и исключив измерение желания). Мы прекрасно знаем, как это работает: когда посреди доклада возникает неловкое место, дыра в повествовании заклеивается фразой наподобие «Как говорил Лакан …». Интересно, что здесь авторитет также выступает под именем собственным, сшивая разрывы речи и превращая ее в речь непрерывную. Другим видом «сшитой» речи является цитирование. Когда речь состоит из непрерывного цитирования, то становится проблематично понять, о каком акте здесь идет речь, что в этой речи есть помимо уровня содержания, и что цитирующий обо всем этом думает. Можно найти и другие примеры «сшитой» речи, однако мы не преследуем цели составить их полный список. Нас интересует другой вопрос, возникающий в этой связи, — каким образом можно говорить, не осуществляя этого сшивания? Этот вопрос кажется важным, поскольку, судя по всему, «говорить не сшивая» означает не просто спотыкаться о нестыковки своей речи или фетишизировать их, говоря тем самым «смотрите, как классно у меня разваливается повествование». Иначе говоря, мы могли бы предположить, что «не» из нашего «не сшивать», устроено чуть хитрее, чем можно было подумать изначально.
[1] Необходимость перехода к топологии, безусловно, вызывает вопрос. Несмотря на то, что есть некая точка бессилия языка, не совсем понятно, почему и как топология решает этот вопрос. На данный момент мы оставим этот вопрос открытым, но отметим, что, на наш взгляд, он является одним из самых интересных.
[2] Мы не настаиваем на полном соответствии взглядов Лакана и Фуко. Так, Фуко, говоря о доклассической эпистеме, подразумевает эпоху Ренессанса, тогда как для Лакана скорее существуют периоды «до» и «после» Декарта.
[3] Ж. Лакан «Четыре основные понятия психоанализа».
[4] О появлении означающего, нам, по-видимому, свидетельствует мебиусный характер данной поверхности.
[5] Читатель может найти данный текст на русском языке в 6-м номере Международного психоаналитического журнала. Однако, мы должны указать на то, что перевод по
[6] На самом деле, как мы скажем дальше, это равенство А=А верно для Фреге, но неверно для Лакана, что, как кажется, и проигнорировал Миллер в своем докладе.
[7] Существует два подхода к определению натуральных чисел: одни авторы причисляют ноль к натуральным числам, другие этого не делают. Фреге относится к первой категории авторов.
[8] Здесь мы хотели бы отметить еще один момент. Мы можем не только увидеть, что 1/0 это то же самое что S/S, но и показать другую запись, а именно: 1/S. Лакан говорит о том, что субъект возникает в поле Другого прежде всего в виде единичной черты, которую он предлагает рассматривать как единицу. Именно поэтому размышления по поводу отношений единицы и нуля имеют более важное для нас значение чем просто утверждение подобия их структуры. Более подробный разговор о единичной черте мы отложим на другой раз.
[9] Кажется, что этот вопрос заслуживает быть раскрытым в отдельной статье.
[10] Напомним читателю, что все происходит за 5 лет до появления теории дискурсов. Поэтому, пусть читатель не удивляется, что место аналитика артикулировано подобным образом.
Автор — Алексей Зайчиков
Текст написан для группы Lacan et autour de lui
