Человек испокон веков искал в окружающем мире порядок. Каждая вещь остается непознанной, покуда рассматривается сама по себе, в отрыве от всего многообразия явлений. Именно взаимосвязи и соотношения разных вещей позволяют определить каждую из них. Слово «определить» здесь подходит как нельзя лучше: ведь оно происходит от слова «предел», то есть граница. Соотнося два предмета (или идеи, свойства, силы) друг с другом, мы отыскиваем их сходства и различия и тем самым узнаем, где заканчивается один, и где начинается другой. Благодаря проведению границ и связей в хаотичном аморфном мире для нас возникает ясность — теперь это мир порядка и законов. А где есть законы, там есть и уверенность, поскольку их знание позволяет понимать прошлое и прогнозировать будущее.

Это простое соображение, по-видимому, всегда двигало человеческий ум к познанию. И история подтвердила, что такое движение не было напрасным. Везде, где открываются законы, рождается наука, а она в свою очередь позволяет поднять всю жизнь человека на качественно новый уровень.

Впрочем, в сегодняшнем мире слово «наука» у многих вполне справедливо ассоциируется с материализмом и уходом от духовных ценностей. Очевидно, что и наука, слишком цепляясь за частичные истины, которые она сумела открыть, может не разглядеть за ними нечто более глубокое и важное. В этой статье речь пойдет о фактах, на которые современная наука обращает мало внимания, но которые тем не менее приближают нас к раскрытию еще более глобального и всеобъемлющего порядка в мироздании.

Золотое сечение и числа Фибоначчи

Об удивительном числе φ (фи), или так называемом «золотом сечении», написано уже немало книг. Определить его можно следующим образом: представьте себе отрезок любой длины. Его нужно поделить так, чтобы меньшая его часть относилась к большей так же, как большая относится ко всему этому отрезку. Это отношение как раз и выражают в математике греческой буквой φ, и равно оно 0,618033… Это бесконечная десятичная дробь.

Ученые заинтересовались этим числом уже давно. Как показал анализ различных архитектурных построек и произведений искусства, мастера древности знали о нем и намеренно использовали его в своих работах. Это же число встречается в расположении листьев на многих растениях, в особенностях строения раковин моллюсков и еще множестве явлений живой природы. Человеческое тело — тоже не исключение: пропорции между различными его частями весьма точно описываются числом φ.

Одним из математических способов, приводящих к этому числу, являются «числа Фибоначчи». Они называются так в честь итальянского математика Леонардо Пизанского, жившего в 1170-1250 годы, который наиболее известен по прозвищу Фибоначчи. Числовой ряд образуется по очень простому принципу. Возьмите вначале два первых натуральных числа: 1 и 2. Их сумма даст 3. Затем сложите 2 и 3, и вы получите 5. Таким образом, каждый раз прибавляя к последнему числу предпоследнее, вы будете двигаться дальше по этому ряду, уходящему в бесконечность.

Каждое отношение двух следующих друг за другом чисел дает число φ, причем с нарастающей точностью. Результаты этих промежуточных отношений будут поочередно то больше, то меньше φ, но с каждым шагом в числовом ряду мы будем подходить все ближе к искомой величине. Следующие примеры проиллюстрируют сказанное:

Числа Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 и т. д.

1 / 2 = 0,5

2 / 3 = 0,666

3 / 5 = 0,6

5 / 8 = 0,625

8 / 13 = 0,615

13 / 21 = 0,619

21 / 34 = 0,618

Таким образом, на последнем из этих шагов мы уже подошли к искомому числу с точностью до тысячных долей.

Золотое сечение является одним из наиболее загадочных математических отношений наряду с числом π (Пи — отношение длины окружности к ее диаметру) и некоторыми другими, все тайны которых еще никем не открыты. Вскоре оно поможет нам в некоторой степени «структурировать» свои представления о солнечной системе. Геометрически это число в наибольшей степени нашло свое выражение в знаке Пентаграммы.

Пылающая звезда — пентаграмма

Пятиконечная звезда с древнейших времен была центральным магическим и священным знаком. Ее можно найти на печатях древних царей и, проходя через всю историю человечества, на самых разных символах и сооружениях. Парацельс, знаменитый алхимик, астролог и маг XVI века, утверждал, что пентаграмма и гексаграмма являются фактически единственными символами, обладающими подлинной силой, причем из этих двух он считал пентаграмму превосходящей по своему могуществу.

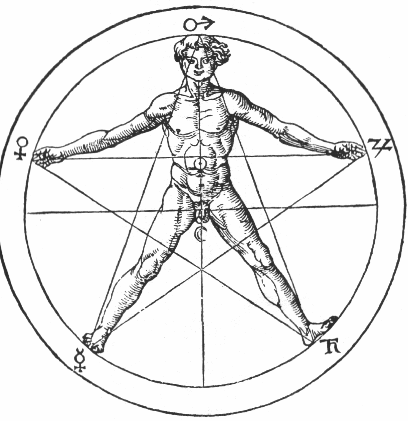
Пентаграмму также иногда называют звездой Давида. В еврейской традиции «щитом Давида» обычно именуется как раз гексаграмма, тогда как для пентаграммы нет особого названия. Это создает некоторую путаницу для тех, кто не достаточно разбирается в традиционных текстах. Еще одно имя пентаграммы — «пылающая (или пламенеющая) звезда», которым часто наделяли ее в оккультных источниках. Как будет показано далее, эта фигура имеет особое отношение к Венере и, в силу специфики последней, она вполне заслуженно может носить такое имя.

Пентаграмма — также знак Микрокосма, или «малого мира». Этим выражением называют человека, который, как гласит традиция, был создан по образу Бога. Бог же, будучи творцом всего мироздания, запечатлел Свой образ на всем творении. Поэтому большой мир аналогичен малому, и человек, изучая себя, может раскрыть загадки Вселенной. «Из плоти моей узрю Бога», — говорится в книге Иова (19:26). Лучи пентаграммы представляют собой руки, ноги и голову вписанного в нее человека, как это показано на иллюстрации из «Оккультной философии» Г.К. Агриппы.

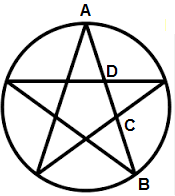
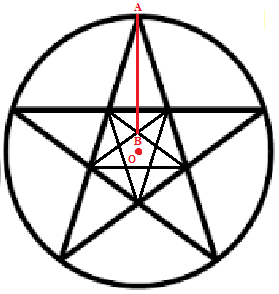
Почему же оккультизм проявляет к этой фигуре такое повышенное внимание? Ответ на это начнем с факта, уже достаточно широко известного современным интеллектуалам: пентаграмма во всех своих частях передает золотое сечение. Возьмем для примера отрезок, идущий от верхнего угла звезды к ее правому нижнему углу (он обозначен АВ). Точка С делит его в золотой пропорции (т. е. АС / AB = φ). Точно так же сам отрезок АС делится в золотой пропорции точкой D (AD / AC = φ). А следовательно, и CD / AD = φ.

Так уже только на одной стороне пентаграммы можно отыскать золотое сечение трижды. Очевидно, что то же самое будет и с остальными ее сторонами. С геометрической точки зрения пентаграмма — фигура почти настолько же уникальная, как треугольник. Дело в том, что сделать замкнутую фигуру невозможно, не имея хотя бы трех точек на плоскости. По этой причине треугольник становится первой такой фигурой, и именно его изучение обусловило развитие целой математической области — тригонометрии. Благодаря множеству теорем и особых соотношений, найденных для треугольника, человек смог понять и законы других геометрических фигур, а с ними — множество явлений окружающей природы.

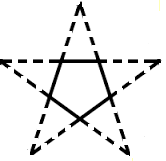
И так же, как треугольник — первая замкнутая фигура (состоящая из прямых отрезков), так пентаграмма является первой фигурой, полученной через «удлинение» выпуклого многоугольника. Если взять равносторонний пятиугольник (пентагон) и провести дальше все его стороны до точек их пересечения друг с другом, получится пентаграмма. Это становится возможным благодаря тому, что стороны пентагона, расположенные через одну, находятся под углом друг к другу.

Если, например, проделать такую же операцию для квадрата, его «удлиненные» стороны, будучи параллельными, никогда не пересекутся. Для треугольника подобная операция также лишена смысла. Зато шести-, семи-, восьмиугольник и т. д. могут подобным образом быть превращены в звезды с таким же числом лучей. Следовательно, пентаграмма — первая геометрическая звезда, «прокладывающая путь» остальным.

К этим интересным наблюдениям, а заодно и к числам Фибоначчи, мы вернемся чуть позже, а пока рассмотрим вкратце историю того, как ученые в разные времена искали порядок в космосе.

Развитие астрономии

С тех пор, как во II веке н. э. ученый александрийской школы Клавдий Птолемей составил свою знаменитую книгу «Великое математическое построение по астрономии» (или просто «Альмагест»), геоцентрическая модель солнечной системы утвердилась на многие века. В ней каждая из пяти известных в ту пору планет — Меркурий, Венера, Марс, Юпитер и Сатурн — а также Солнце и Луна вращались вокруг Земли по круговым орбитам. Чтобы согласовать эту простую модель с наблюдениями, дававшими гораздо более сложные результаты, к каждой сфере были добавлены эпициклы — малые круги, по которым планета вращалась одновременно с ее движением внутри большой сферы.

В раннее средневековье эту модель у греков переняли арабы, а затем она вновь распространилась в Европе. Поколения астрономов тратили свои жизни на то, чтобы уточнить ее и привести в полное соответствие с наблюдаемым движением планет, однако сделать это со всей точностью никак не удавалось. В наше время любой школьник узнает о том, что центром всей системы планет является Солнце, вокруг которого они вращаются. Это открытие приписывается Николаю Копернику, опубликовавшему в 1543 году трактат «О вращении небесных сфер», где впервые была детально разработана и обоснована гелиоцентрическая система.

Впрочем, сама идея гелиоцентричности имеет гораздо более древние корни. Ее выдвигал еще античный астроном Аристарх (III век до н. э.), однако в ту пору она не получила поддержки. Наблюдение за планетами показывает, что Меркурий не отходит от Солнца более, чем на 28 градусов, а максимальное расстояние Венеры от Солнца составляет около 45 градусов. Этот факт привел к тому, что среди астрономов Средневековья велись нескончаемые споры о реальном местоположении двух этих планет. Уже здесь мы находим элементы гелиоцентрической теории. Сам Коперник, обсуждая данную тему, указывает на это: «Поэтому, я полагаю, никак не следует пренебрегать тем, что написал в энциклопедии Марциан Капелла, и что хорошо знали некоторые другие латинские писатели. Они полагают, что Венера и Меркурий обращаются вокруг находящегося в середине Солнца, и по этой причине думают, что эти планеты могут отойти от Солнца не дальше, чем позволяет кривизна их орбит. Поэтому эти светила не обходят вокруг Земли, как другие планеты, но имеют повернутые внутрь апсиды…» (О вращении небесных сфер, кн. 1, гл. 10).

Желающим проследить за ходом мысли ученых того времени по поводу Меркурия и Венеры стоит прочесть всю главу, из которой приведена эта цитата. Там они найдут аргументы тех, кто размещал эти две планеты «над Солнцем» (то есть считал их орбиты расположенным дальше от Земли, чем солнечная), и тех, кто настаивал на их нахождении «под Солнцем». С точки зрения современной астрономии, которая с тех пор сделала гигантский прорыв вперед, аргументы и той, и другой стороны выглядят крайне нелепо, но, по-видимому, именно изучение Меркурия и Венеры с их спецификой в сравнении с более отдаленными планетами приблизило в ту пору появление гелиоцентрической модели.

Теория Коперника стала новой вехой в развитии представлений человека о космосе. В ней вокруг Солнца вращаются не только Меркурий с Венерой, но и все остальные планеты, включая Землю. Лишь Луна, которая в классической астрономии древности, принималась на одинаковых правах с планетами, осталась вращаться вокруг Земли и с тех пор начала восприниматься как ее спутник. При этом важно отметить, что орбиты всех этих небесных тел изображались в виде кругов, а Солнце попадало точно в центр (для орбиты Луны в центре была Земля). Именно с такой моделью познакомился молодой Иоганн Кеплер в университете Тюбингена, куда он поступил в 1591 году. Кеплер стал пламенным сторонником теории Коперника, и уже в 1596 году он выпустил книгу «Тайна мироздания» (Mysterium Cosmographicum), в которой предпринималась попытка показать математическую гармонию космоса.

Теория Кеплера. Пять платоновых тел

Чтобы понять то, что изложил Кеплер в своей книге, необходимо знать о пяти платоновых телах. В диалоге «Тимей» Платон повествует о пяти правильных многогранниках. Это геометрические тела, все грани которых являются равносторонними (правильными) многоугольниками, при этом все вершины оказываются равноудалены от центра. Таким образом, если описать сферу вокруг такого многогранника, каждая из его вершин окажется на ее поверхности. Если же вписать сферу внутрь него, она коснется середины каждой из его граней.

Платон соотносит эти тела с четырьмя элементами. Самым простым из них является тетраэдр — пирамида, состоящая из четырех равносторонних треугольников (три из них образуют «стены» пирамиды, а четвертая — ее основание). Это тело связывается с элементом огня. Куб, грани которого представляют собой квадраты, соотносится с землей. Октаэдр — восьмигранник из равносторонних треугольников — ассоциируется с воздухом. Икосаэдр с двадцатью гранями в виде равносторонних треугольников представляет элемент воды. И, наконец, пятое тело — додекаэдр, гранями которого являются пентагоны. Он относится к пятому элементу, из которого Творец создал небо.

Более поздние геометрические исследования доказали, что эти пять тел являются единственными возможными правильными многогранниками — никаких других логически существовать не может. В добавок, нам известно, что четыре из этих тел образуют две пары. Если соединить линиями все середины сторон куба, получится октаэдр. Проделав ту же операцию с октаэдром, мы вновь получим куб. Следовательно, два этих тела взаимно трансформируются друг в друга. Аналогичным принципом связаны икосаэдр и додекаэдр. Получается, что земля и воздух (в философии Платона) — взаимно обратимые элементы, и, как ни странно, вода и небесный эфир — тоже. Огонь же в гордом одиночестве не имеет подобной пары (если проделать такую операцию с тетраэдром, получится другой, «перевернутый» тетраэдр).

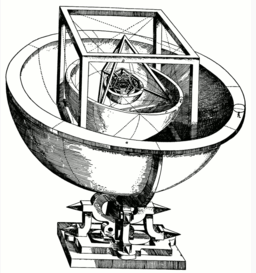
Кеплер, видя между шестью планетами солнечной системы пять промежутков, стал разрабатывать модель, согласно которой в них вписываются платоновы тела. Именно эти тела должны были связать своими размерами орбиты известных в ту пору планет. Как уже было отмечено выше, каждый из правильных многогранников может быть вписан во внешнюю сферу и содержать в себе внутреннюю. Таким образом, он задает строгое отношение этих двух сфер. В орбиту Сатурна по Кеплеру вписывался куб, который охватывал орбиту Юпитера. Далее следовал тетраэдр и орбита Марса, затем — додекаэдр и орбита Земли, икосаэдр и орбита Венеры, октаэдр и орбита Меркурия.

Кеплер, как известно, был не только математиком и астрономом. Он был также астрологом и оккультистом. Именно он ввел в астрологию так называемые «минорные» аспекты — квинконс и полусекстиль. Его модель с пятью платоновыми телами оказалась неудовлетворительной — погрешность между ее пропорциями и реальными размерами орбит была слишком велика. Кроме того, занимаясь ее разработкой, Кеплер еще не знал о том, что предстоит ему открыть в последующие годы. Получив записи наблюдений астронома Тихо Браге, он пришел к выводу, что орбиты планет представляют собой не круги, а эллипсы. Вначале этот вывод был применен только к Марсу, но позже он подтвердился и для других планет. Вслед за этим были открыты известные по сей день три закона движения планет. Этот вклад в астрономию наука приняла и использует до сих пор, тогда как поиски космической гармонии ортодоксальных ученых не интересуют. Сам Кеплер, тем не менее, всю свою жизнь не оставлял попыток отыскать ее и в 1621 году переиздал книгу «Тайна мироздания» с поправками и дополнениями.

Правило Тициуса — Боде

Прошло более 150 лет с тех пор, как Кеплер выдвинул свою теорию. Конечно же, за это время многие занимались данной проблематикой и изучали законы строения Вселенной. Но здесь мы ограничимся наиболее известными и значимыми работами. В 1766 году И.Д. Тициус предложил правило, согласно которому все орбиты планет солнечной системы выстраиваются в связную закономерную картину. Несколькими годами позже его опубликовал И.Э. Боде (в честь этих двух ученых оно получило свое название).

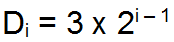
Чтобы понять, как работает данное правило, нужно построить геометрическую прогрессию: ее нулевой элемент равен нулю, а начиная с первого работает формула:

Так получается ряд чисел 0, 3, 6, 12, 24, 48, 96, 192, 384 и т. д.

Теперь, если к каждому из этих чисел прибавить 4, а затем поделить результат на 10, мы получим среднее расстояние от Солнца до планеты i, выраженное в астрономических единицах (за 1 такую единицу принято среднее расстояние от Солнца до Земли).

Полученные числа действительно довольно точно соответствуют реальным планетарным орбитам. Когда это правило было предложено, на него обратили мало внимания, но буквально через несколько лет после этого (в 1781 году) был открыт Уран, и оказалось, что его орбита находится именно там, где должна быть согласно правилу Тициуса-Боде. Между Марсом и Юпитером оставалась пустая «ячейка» — на расстоянии 2,8 а. е. не было никакой планеты. Начав искать в этой области неба, астрономы вскоре обнаружили Цереру. Сегодня ее считают карликовой планетой, принадлежащей к поясу астероидов между Марсом и Юпитером.

Эти успехи укрепили доверие к правилу Тициуса-Боде. Однако в дальнейшем ученых поджидала неудача. Открытый в XIX веке Нептун «не вписался» в общую закономерность. Вместо него гораздо позже в нужную «ячейку» попал Плутон. Кроме того, точность данных, получаемых согласно этому правилу, хотя и относительно высока, все же имеет заметное расхождение с действительностью.

Отношение к правилу Тициуса-Боде в современной науке уже довольно скептическое, однако более поздние разработки зачастую принимают во внимание полученные с его помощью факты и стараются объяснить их по-своему. Здесь уместно упомянуть теорию орбитальных резонансов и другие направления в современной астрономии.

Однако, описав вкратце научные шаги в поиске единой картины космоса (или по меньшей мере солнечной системы), мы возвращаемся к тому, с чего начали, — к сакральной геометрии и оккультному подходу.

Астрономические «совпадения»

В пентаграмме, как уже говорилось, много раз встречается золотое сечение. В частности, если внутри пятиугольника, образованного пересечением лучей пентаграммы, изобразить еще одну маленькую пентаграмму, соединяющую его углы, она будет соотноситься с большой пентаграммой как φ в квадрате, то есть как если бы мы взяли у этой большой пентаграммы золотое сечение от золотого сечения.

В таком же точно соотношении находятся физические размеры Земли и Меркурия. Любой учебник по астрономии покажет вам, что окружность земного экватора равна 40075 км, а у Меркурия — 15329 км. Простые вычисления приведут нас к очевидному выводу:

0,618×0,618 = 0,382

15329 / 40075 = 0,382

Более того, средние размеры орбит (то есть большая полуось орбитального эллипса — среднее расстояние от Солнца) Земли и Меркурия имеют почти такое же соотношение — 0,387. Фактически это означает, что если мы проведем окружность через углы пентаграммы, а затем еще одну через углы ее внутреннего пятиугольника, две эти окружности будут соотноситься как Земля с Меркурием (по размерам) и как орбита Земли с орбитой Меркурия.

Теперь перейдем к Венере. Эта удивительная планета совершает 13 оборотов вокруг Солнца за то же время, за какое Земля делает 8 своих оборотов. Сидерический период Венеры (ее «год») длится 224,7 земных суток, а земной год, как известно, равен 365,25 суток. Раз в 583,9 суток Венера оказывается точно между Землей и Солнцем (такова длительность ее синодического периода). Следовательно, за этот цикл из 8 земных лет наша планета сближается с Венерой ровно 5 раз.

Все эти числа — 5 сближений, 8 земных лет, 13 лет Венеры — не напоминают ли они нам о чем-то знакомом? Да ведь это же идущие друг за другом числа из ряда Фибоначчи! И, конечно же, начав анализировать соотношение земной и венерианской орбит, мы быстро откроем и там закон золотого сечения и пентаграммы. Если поставить Землю в центр пентаграммы (точка О на рисунке), а за радиус описывающей ее окружности взять максимальное расстояние между Землей и Венерой (отрезок ОА), то минимальное расстояние будет выражаться отрезком ОВ, идущим от центра до угла внутреннего пятиугольника малой пентаграммы. Таким образом, отрезок АВ был бы диаметром того, что древние астрономы назвали бы эпициклом Венеры.

Также, если изобразить графически траекторию движения Венеры относительно Земли, получится красивый «цветок» с пятью лепестками. Соединив кончики этих лепестков прямыми линиями, мы получим пентаграмму. Венера каждые несколько лет вырисовывает этот магический знак вокруг нашей планеты.

Выше уже говорилось, что выражение «пылающая звезда» как нельзя лучше подходит к Венере. Ведь это самая яркая «звезда» на нашем небосклоне. Ее хорошо видно невооруженным глазом — она всегда украшает вечернее небо на закате или утреннее перед восходом. В еврейском языке она называется "נוגה" (нога), что означает «сияющая».

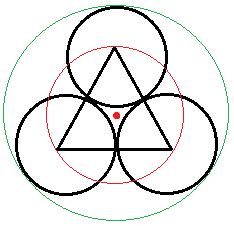
Если исключить из рассмотрения Землю и проанализировать расстояния от Меркурия и Венеры до Солнца, здесь тоже откроется интересное соотношение. Представьте себе треугольник, в центре которого расположено Солнце, а углы находятся на средней орбите Меркурия. Если провести три окружности с центрами в углах этого треугольника так, чтобы они соприкасались между собой, то расстояние от центра до наиболее удаленных точек этих окружностей будет равно расстоянию от Солнца до Венеры. Иными словами, половина стороны такого треугольника будет равна расстоянию от средней орбиты Меркурия до орбиты Венеры.

(В этой статье я неоднократно использую выражение «средняя орбита Меркурия». Это связано с тем, что у этой орбиты большой эксцентриситет — 0,206, и потому ее эллипс заметно вытянут в сравнении с кругом. Что же касается орбит Венеры и Земли, их эксцентриситет настолько мал (0,007 для Венеры и 0,017 для Земли), что им можно пренебречь. Для этих планет, чья орбита почти идентична кругу, наибольшее и наименьшее расстояния от Солнца не так уж сильно отличаются).

Соотношения между другими астрономическими величинами, в том числе связанными и с более удаленными от Солнца планетами, также открывают перед исследователем точные геометрические пропорции. Именно в нахождении этих пропорций (не только для планет, но и для всей природы) древние видели «сакральную» (то есть священную) геометрию, помогающую понять замысел Творца мира — великого Архитектора.

«Человек — мерило всех вещей»

До сих пор мы находили лишь отдельные любопытные факты, связанные с астрономическими величинами. Можно ли объединить их в общую картину? И что будет являться основой для такого обобщающего построения?

Как уже отмечалось выше, с древнейших времен человек мыслился мудрецами как «микрокосм» — малый мир, отражающий в себе структуру Вселенной. Античные философы называли его «мерилом всех вещей», потому что с его помощью можно измерить пропорции окружающего мира. Тора утверждает, что Бог создал человека по Своему образу. Однако здесь возникает вопрос: существует ли метод, позволяющий использовать данные о строении человека? И где мы можем найти эти данные?

Для тех, кто хорошо знаком с оккультной традицией, ответ очевиден. Действительно, с древних времен этим вопросам уделялось пристальное внимание. Хотя люди бывают разные — толстые и худые, высокие и низкие — тем не менее существуют идеальные пропорции, описывающие тело человека.

С древних времен до нас дошли «Десять книг об архитектуре» римского ученого Витрувия, жившего во времена Юлия Цезаря. Его перу принадлежит описание базовых пропорций тела. Хотя его книга посвящена строительству зданий, он уделяет внимание и устройству человека, поскольку в архитектуре должны соблюдаться такие же размеры:

«Дело в том, – пишет Витрувий, — что никакой храм без соразмерности и пропорции не может иметь правильной композиции, если в нем не будет такого же точного членения, как и у хорошо сложенного человека» (Десять книг об архитектуре, кн. 3, гл. 1, п. 1).

Вслед за этим автор начинает перечислять эти пропорции:

«Ведь природа сложила человеческое тело так, что лицо от подбородка до верхней линии лба и начала корней волос составляет десятую долю тела, так же как и вытянутая кисть от запястья до конца среднего пальца. Голова от подбородка до темени — восьмую, и вместе с шеей, начиная с ее основания от верха груди до начала корней волос, — шестую, а от середины груди до темени — четвертую… Ступня составляет шестую часть длины тела, локтевая часть руки — четверть, и грудь — тоже четверть… Далее, естественный центр человеческого тела — пупок. Ибо, если положить навзничь человека с распростертыми руками и ногами и приставить ножку циркуля к его пупку, то при описании окружности линия ее коснется пальцев обеих рук и ног. Точно так же, как из тела может быть получено очертание окружности, из него можно образовать и фигуру квадрата. Ибо если измерить расстояние от подошвы ног до темени и приложить эту же меру к распростертым рукам, то получится одинаковая длина и ширина, так же как на правильных квадратных площадках» (там же п. 2-3).

Для древнего мира вообще было очень характерно использование естественных мер для измерения любых величин. Длину измеряли локтями, ладонями (пядями) и пальцами. Объем мерили яйцами, оливками, финиками, ячменными зернами и т. д. В законах иудаизма, например, сформулированных еще мудрецами Талмуда (I — V века н. э.), количество съеденной пищи, после которого требуется произносить благословение, определяется «как оливка» (т. е. размером с оливку) или «как яйцо». В День искупления (Йом Кипур) Тора повелевает «истязать души ваши», то есть поститься, отказывая себе в еде. Наказание (карет) для тех, кто нарушает этот запрет, предусмотрено в случае, если человек съел «как большой финик» пищи. Таких примеров можно привести множество.

Точно так же все строительные величины для переносного храма (мишкана), сооруженного евреями в синайской пустыне, и для иерусалимского храма указаны в локтях. Очевидно, ими же определялись размеры и других сооружений в различных древних культурах. Об этих мерах Витрувий пишет следующее:

«Кроме того, за основание мер, явно необходимых при всяких строительных работах, они взяли также члены тела, как палец, пядь, ступню, локоть и распределили их по совершенному числу, называемому греками τελεον. А совершенным числом древние установили число десять, ибо оно определяется числом пальцев на руках… Вышина тела определяется числом шести ступней. И заметили, что локоть состоит из шести пядей или двадцати четырех пальцев» (там же п. 6-7).

Легко доказать, что пропорции, данные Витрувием, в точности совпадают с принятыми в еврейской традиции. В Талмуде упоминания об этих размерах разбросаны по различным трактатам и встречаются множество раз. В XII веке кодификатор Алахи (законов иудаизма) рав Моше бен Маймон, известный как Рамбам или Маймонид, сформулировал обобщение, касающееся этих величин (Законы тфилин, гл. 9, п. 9):

«Ширину пальца во всех этих размерах, как и в остальных размерах Торы, мы уже уточнили и нашли, что она равна ширине семи средних зерен ячменя, тесно прижатых друг к другу. Это равно длине двух зерен, лежащих свободно. Ладонь (тефах) в любом месте равна четырем пальцам, а каждый локоть (ама) — шести ладоням».

Итак, получаются следующие отношения:

1 локоть = 6 ладоней (пядей) = 24 пальца;

1 ладонь = 4 пальца;

1 ступня = 4 ладони = 16 пальцев.

Последняя строка базируется на том, что, как приведено выше от имени Витрувия, локоть является одной четвертой частью тела, а ступня — одной шестой. Если вытянуть руки в стороны, то от конца среднего пальца до локтевого сустава будет четверть всей длины; от сустава до середины груди — еще четверть; оттуда до локтевого сустава второй руки — еще четверть; и от него до конца пальца — последняя четверть. Такими же четырьмя локтями измеряется и высота тела человека от ступней до темени (на этом основана квадратная мера в рассуждениях Витрувия).

Очевидно, именно этот размер стал основанием для столь часто используемого талмудического выражения «четыре локтя». Оно встречается в огромном количестве законов иудаизма. К примеру, на дом, площадь которого меньше 4×4 локтя, не нужно вешать мезузу, для него не нужно строить перила, в него не кладут эрув (разрешающий переносить предметы в шаббат в общем дворе) и т. д. Фактически Алаха не признает за ним статус дома (см. трактат Сукка 2 б — 3 а). Точно так же, согласно одному из мнений, размером 4×4 локтя должна обладать сукка (шалаш, который заповедано сооружать на осенний праздник Суккот). Четыре локтя образуют вокруг человека пространство, внутри которого он может приобретать предметы, не имеющие хозяина.

Не зная об этих замечательных соотношениях, невозможно, к примеру, понять такое высказывание из Талмуда: «С тех пор, как был разрушен храм, нет у Святого, благословен Он, в мире ничего, кроме четырех локтей закона» (трактат Брахот 8 а). Очевидно, все эти еврейские законы, использующие меру в 4 локтя, основаны на том, что они составляют рост человека. Поэтому в некоторых случаях выражение «четыре локтя» фактически становится синонимом слова «человека» и полностью заменяет его. Когда же речь идет о площади в 4 квадратных локтя (как, например, в законах о доме и о сукке), их основание кроется в том, что человек равен 4 локтям и по длине, и по ширине. Иными словами, дом может считаться настоящим домом лишь в том случае, если в него можно уложить человека во весь рост с раскинутыми в стороны руками.

Сакральная геометрия в применении к космосу

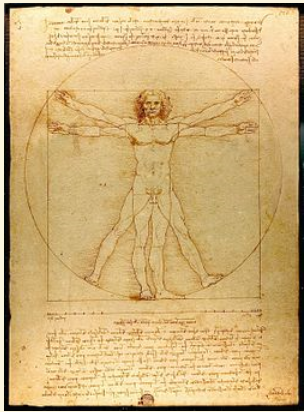
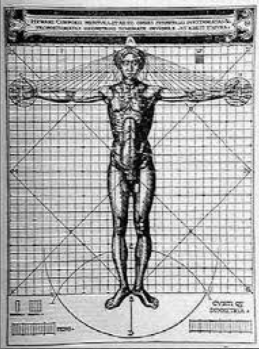
По-видимому, в средневековой Европе немногие интересовались сакральной геометрией и поиском мировой гармонии. Однако наступивший вслед за тем ренессанс заново открыл эти направления исследований. Леонардо да Винчи в XV веке подробно изучал пропорции человеческого тела. Его знаменитый рисунок «Витрувианский человек» помогает наглядно увидеть то, что за полторы тысячи лет до него описал римский архитектор. Затем, уже в XVI веке, появляется книга «Оккультная философия» Агриппы (уже упоминавшаяся нами ранее), где даны дополнительные телесные пропорции. В частности, ее автор отмечает следующее:

«Девять мер ширины лица образуют широкого коренастого человека, а десять — высокого. Если поделить высоту человека на девять частей, получится следующее. Лицо от вершины лба до низа подбородка — одна часть; от нижней части горла или вершины груди до вершины живота — вторая; оттуда до пупка — третья; оттуда до низа бедра (до конца ягодиц) — четвертая; оттуда все бедро до вершины икры дает две части; оттуда до сустава ступни — еще две. Все это вместе образует восемь частей. Сверх этого, пространство от вершины лба до макушки, и от подбородка до вершины груди, и от сустава ступни до подошвы ступни, — я говорю, три эти пространства, соединенные вместе, образуют девятую часть. Грудь в ширину имеет две части, а обе руки — семь.

Но такое тело, которое составляют десять мер ширины лица, имеет наиболее точные пропорции. Первая его часть — от макушки до низа носа; оттуда до вершины груди — вторая; далее до вершины живота — третья; оттуда до пупка — четвертая; оттуда до половых органов — пятая, и там находится середина человеческого роста. Оттуда до подошв ступней расположены еще пять частей, которые, будучи соединены с предыдущими, образуют целые десять частей, которыми каждое тело измеряется наиболее пропорциональным образом» (Оккультная философия, кн. 2, гл. 27).

В этом длинном описании стоит обратить особое внимание на расположение пупка. В «наиболее точных пропорциях» он находится в точке, представляющей 0,4 тела (сверху) или 0,6 тела (снизу). Для «коренастого человека», все тело которого образовано девятью мерами ширины лица, пупок будет чуть выше — примерно в области золотого сечения. Некоторые современные авторы как раз об этом и заявляют, однако Агриппа признает первый вариант наиболее точным. И давайте не забывать, что именно пупок Витрувий назвал «естественным центром человеческого тела».

В солнечной системе эта величина повторяется много раз. Если мы поставим воображаемого человека ногами на Солнце, а его макушка упрется в Марс, находящийся в афелии, то Земля окажется у него в пупке. Посчитать это не составляет труда:

Афелий Марса = 1,666 а. е.

Афелий Земли = 1,017 а. е.

1,017 / 1,666 = 0,61

Здесь мы имеем пупок «коренастого человека». По моим вычислениям наиболее точный «пупок» находится на высоте 0,603 от подошвы ног. Именно в таком «пупке» оказывается Церера в афелии по отношению к Юпитеру в перигелии:

Афелий Цереры = 2,984 а. е.

Перигелий Юпитера = 4,95 а. е.

2,984 / 4,95 = 0,603

То же самое получим, если возьмем отношение афелия Юпитера к перигелию Сатурна:

Афелий Юпитера = 5,458 а. е.

Перигелий Сатурна = 9,048 а. е.

5,458 / 9,048 = 0,603

Теперь возьмем отношение перигелия Урана к афелию Нептуна:

Перигелий Урана = 18,376 а. е.

Афелий Нептуна = 30,441 а. е.

18,376 / 30,441 = 0,603

А если вам и этого мало, посчитайте заодно отношение перигелия Нептуна к афелию Плутона, и вы получите:

Перигелий Нептуна = 29,766 а. е.

Афелий Плутона = 49,305 а. е.

29,766 / 49,305 = 0,603

Эти данные являются лишь скромными фрагментами в гораздо более обширной картине. Чтобы увидеть подробнее место каждой планеты, следует рассматривать не только пупок, но и солнечной сплетение, половой орган, колени и щиколотки нашего воображаемого человека. В свою очередь отношение его макушки с концом носа или ртом поможет увидеть, как соотносятся перигелий и афелий у одной и той же планеты (для некоторых планет). Подробный анализ потребовал бы слишком много места, да и не стоит отнимать у любознательного читателя возможность самому отыскать эти удивительные закономерности нашего мира. Важно лишь отметить следующее: устройство Вселенной — не случайный набор величин. Она связана законами, многие из которых современной науке еще не известны. А древний принцип аналогии микро- и макрокосма — возможно, самый универсальный ключ к раскрытию этих секретов.