Лауреаты ежегодной премии «Просветитель» будут объявлены 19 ноября. В шорт-лист премии вошли восемь авторов, четыре — в номинации «Естественные науки», четыре — в номинации «Гуманитарные науки». На «Сигме» будут опубликованы интервью с номинантами премии, а также отрывки из их книг

Книга «Математическая составляющая» частично опубликована на сайте издательства в электронном виде. Приобрести ее можно в Доме книги «Молодая гвардия» и магазине «Математическая книга».

Интервью с авторами издания

Предисловие

То, что математика является и языком, и главным инструментом естественных наук и техники, читателю известно. В географических представлениях древних народов для земного диска и опорой, и двигателем служила гигантская черепаха. Математика играет сходную роль и в физике, от теории до приложений, и в осуществлении космических полётов, и в укрощении атомной энергии, и в жизни компьютерного мира. Менее очевидна для широкой публики важность математики в таких дисциплинах, как медицина или лингвистика.

Но даже читатель, догадывающийся о значительной математической «составляющей» в различных сферах деятельности, не всегда может оценить степень зависимости этих областей от математики. Основная причина—сложность применяемых математических инструментов, часто—специально разработанных для конкретного приложения. И признавая на словах роль математики, люди редко задумываются над математической «начинкой» окружающих нас предметов и явлений, а иногда и просто не замечают её.

Существующие прикладные задачи являются постоянным и требовательным заказчиком, ставящим всё новые и новые проблемы для самой математики. С другой стороны, прогресс в математике открывает новые возможности, порождает такие технические задачи и решения, о которых до того нельзя было и подозревать. Но бывает и так, что результаты теоретической математики ждут своего практического «воплощения» долгими десятилетиями, а потом «выстреливают» эффектно и с невероятной эффективностью. Ряд примеров такого двустороннего взаимодействия читатель найдёт в этой книге.

Книга состоит из трёх частей, каждая имеет свой цветовой код.

В первой («синей») части собраны короткие тексты, демонстрирующие жизненную необходимость для человечества математических исследований.

Во второй («зелёной» и самой простой) части содержатся математические «проявления» в повседневной жизни. Большинство сюжетов — из математического фольклора, они приводятся в обработке составителей сборника.

В первых двух частях формул почти нет, просмотреть их и ощутить необходимую и незаменимую роль математики в жизни современного общества сможет любой читатель. Нам кажется, что такое представление должны получить самые широкие круги читателей, и, в особенности — те, кто принимает важные решения: от школьника, выбирающего свою будущую профессию, до государственного деятеля, определяющего приоритеты в развитии страны.

Третья часть книги рассчитана на более подготовленного читателя, одним из главных желаний которого стало бы выяснение сути используемого математического «механизма». Тексты могут отличаться от материалов других частей сборника большей детализацией изложения и объёмом статей, содержать более сложные математические «подробности». Отметим, что некоторые материалы — расширение и углубление разговора, начатого в первой части книги. Для этих материалов тексты из первой части служат общедоступным введением.

Но у материалов всех частей книги есть и общая черта. По замыслу составителей, пёстрый калейдоскоп представленных сюжетов должен познакомить читателя с тем особым взглядом на мир, который отличает математиков. Это не только развитое логическое мышление, владение различными математическими инструментами в виде формул, теорем и теорий, но и умение видеть, находить, использовать общие свойства разнородных явлений. Надеемся, что примеры из сборника позволят читателю почувствовать и оценить подобный подход к изучению окружающего нас мира.

Особенность книги — то, что многие статьи для первой и третьей частей написаны российскими математиками, результаты которых определяют мировой уровень математики. Для читающей публики получение научной информации из первых рук — редкая удача.

Появление известных математиков как авторов на страницах этой книги объясняется тем, что она создавалась в Математическом институте имени В.А. Стеклова РАН—ведущем научном центре страны. Традицией российского математического сообщества является деятельное участие в организации математического образования, борьба за сохранение уровня в этом важном деле. Поэтому просьбы составителей к коллегам находили отклик доброжелательный, заинтересованный, деятельный.

Чтобы не отпугнуть читателя, опасающегося текстов с формулами и теоремами, для данного сборника сознательно выбран популярно-описательный стиль изложения. Понятно, что у части читателей такой стиль может вызвать ощущение недостаточной строгости и чёткости. Авторы старались этого избежать. В случае выявления неточностей изложения и прочих погрешностей, просьба относить их исключительно к недоработке редакторов-составителей.

Важной составляющей данного сборника являются рисунки. И рисунки, и весь графический стиль оформления книги созданы Романом Кокшаровым. Математическая точность рисунков, вёрстка книги — заслуга Михаила Панова.

Расширенная электронная версия сборника находится на сайте «Математические этюды» по адресу http://etudes.ru. Электронная версия дополнена ссылками на другие источники по темам, представленным в книге.

Математические факты, на которых основаны сюжеты второй части, вдумчивый читатель сможет восстановить и проанализировать самостоятельно. Подобный сценарий может использовать и учитель, который найдёт здесь богатый материал для работы со школьниками.

Подчеркнём, что сам сборник не состоялся бы без работы над проектом «Математические этюды», который, в свою очередь, реализован благодаря самоотверженному труду Михаила Калиниченко, Романа Кокшарова, Никиты Шавельзона.

Книга не претендует на роль полного, универсального сборника примеров проявления математики в жизни. В выборе представленных тем отражены вкусы авторов и составителей сборника. За бортом осталось множество ярких примеров, о которых просто необходимо рассказывать. Надеемся, что в сотрудничестве с читателями эта работа будет продолжена.

Редакторы-составители:

Николай Николаевич
Андреев Сергей
Петрович Коновалов
Никита Михайлович Панюнин
сотрудники лаборатории
популяризации и пропаганды математики
Математического института имени В.А. Стеклова РАН

Математика интернета

Странное название, скажет читатель, проводящий часть жизни в интернете. Ведь возникновение сайтов, их наполнение контентом, установление связей между ними (ссылки)—всё это происходит стихийно, никем явным образом не управляется. Но как и другие сложные системы, состоящие из большого числа «свободных» элементов, интернет становится средой, в целом имеющей устойчивые свойства, не зависящие от беспорядка в мелочах, и поддающиеся исследованию математическими методами.

Будем представлять интернет в виде графа. Граф — это множество точек (вершин графа), соединённых конечным числом дуг (рёбер графа). Вершинами будем считать интернет-сайты, а рёбрами—гиперссылки, идущие с одних сайтов на другие. Рёбра этого графа—ориентированные (в ссылках важно кто на кого ссылается), некоторые из них — кратные (несколько ссылок с одного сайта на другой), есть и петли (ссылки между страницами одного и того же сайта).

Построенный веб-граф — настоящий монстр с миллиардами вершин и рёбер. Этот граф постоянно меняется: добавляются и исчезают сайты, пропадают и появляются ссылки. Но при всех изменениях, некоторые свойства интернета остаются неизменными на протяжении всей истории его исследования. Вот несколько примеров таких «устойчивых» свойств.

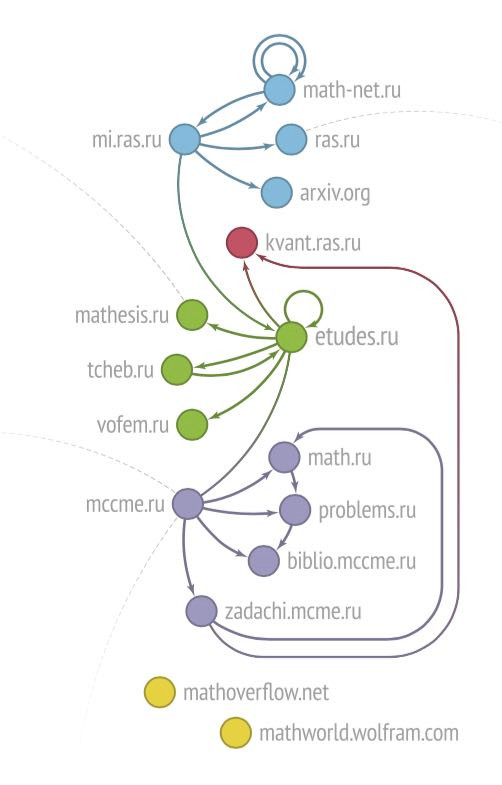
Веб-граф разрежен. В нём лишь в несколько раз больше рёбер, чем вершин. Казалось бы, странное дело — возможны любые ссылки, а рёбер всё равно мало.

Несмотря на разреженность, интернет-мир очень тесен. А именно, от любого сайта до любого другого можно по ссылкам перейти за 5—6 «кликов»

(знаменитый закон «шести рукопожатий»).

В веб-графе высока вероятность того, что «соседи» данной вершины (сайты, связанные ссылками с данным) сами связаны ребром: «мои знакомые знакомы между собой».

Важная характеристика вершины графа — её степень, т.е. число входящих и выходящих рёбер. Оказывается, что степени вершин «правильно», т.е. по определённому закону, распределены: доля вершин данной степени d пропорциональна величине 1/dγ, где γ ≈ 2,3. В этой формуле есть понятное ядро — доля вершин большой степени d (сайтов с большим количеством ссылок) мала. Но есть и удивительная деталь — постоянная γ не зависит от числа вершин веб-графа, т.е. не меняется в процессе развития интернета. Этот степенной закон является универсальным для сложных сетей — от биологических до межбанковских, разве что для разных сетей величина γ немного разная.

Интернет как целое устойчив к случайным атакам на сайты. А именно, если уничтожение сайтов происходит независимо и с одинаковой вероятностью, то веб-граф с вероятностью, близкой к 1, сохраняет «гигантскую» связную компоненту. Эта компонента сохраняется даже при прицельной атаке на хабы—вершины наибольших степеней — пока доля атакованных хабов не превысит некоторое критическое значение.

Для изучения интернета необходимо уметь строить модель «случайного графа», которая с высокой вероятностью обладает ожидаемыми свойствами реального интернета. При этом для практических нужд, да и для чисто математических целей, крайне важно, чтобы модель не была слишком сложной. Эта трудная и привлекательная задача полностью не решена.

Построение хорошей математической модели интернета сразу же даёт качественно новые инструменты для улучшения информационного поиска, выявления спама, прогнозирования распространения информации в социальных сетях и в интернете в целом.

С другой стороны, математические модели интернета оказываются весьма похожими на модели биологических сообществ или модели межбанковского взаимодействия. И хотя изучение биологических или финансовых сообществ началось значительно раньше, чем появился интернет, интенсивность развития последнего и достижения в его изучении делают влияние всех этих моделей взаимно-благотворным.

Поэтому математика интернета востребована и биологами (предсказание эпидемий), и создателями лекарств (бактериальные сообщества, живущие в организме человека, тоже похожи на интернет), и финансистами (риски возникновения кризисов).

Изучение подобных систем—один из центральных разделов прикладной математики и неиссякаемый источник новых задач для всей математики.

Компьютерная томография—одно из наиболее впечатляющих научных достижений ХХ века. Оно оказало революционное воздействие на всю современную медицину. За разработку компьютерной томографии А. Кормак и Г. Хаунсфилд были удостоены Нобелевской премии 1979 года в области медицины и физиологии.

Компьютерная томография

При снятии томограммы изучаемую часть тела человека микросдвигами перемещают сквозь кольцо сканирующего устройства. Сканер, состоящий из источника рентгеновского излучения и ряда детекторов, находится в корпусе, имеющем форму тора («бублика») и может вращаться в нём по кругу.

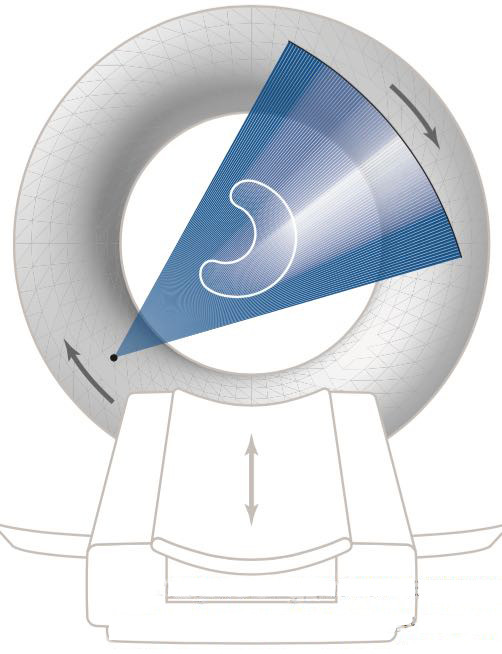
На древнегреческом «τo ́μoς» означает «сечение». При фиксированном относительно томографа положении тела происходит следующее. При каждом повороте сканера из источника излучения веером «выходят» лучи, а данные детекторов характеризуют ослабление излучения вдоль соответствующих направлений. Коэффициент поглощения в каждой точке зависит от плотности тканей организма, а интеграл от функции «коэффициент поглощения» по отрезку «движения» луча от источника до детектора определит суммарное поглощение луча. Если по значениям таких интегралов удастся восстановить значения интегрируемой функции, то в рассматриваемом сечении человеческий организм будет представлен «картой» плотности тканей. Набор изображений, полученных в серии параллельных сечений, даёт трехмерное представление. Расположение и размеры участков с «неправильно» изменённой плотностью позволяют врачу поставить диагноз.

С математической точки зрения восстановление функции на плоскости по её интегралам вдоль всевозможных прямых — классическая задача, решённая Иоганном Радоном в 1917 году. Однако практическая реализация томографических возможностей формулы Радона стала возможной только с приходом эры компьютеров. Задача является трудной не только из–за гигантского объёма данных, для её решения помимо компьютеров потребовались математические методы, развивавшиеся в течение всего XX столетия. Отметим, что высокая стоимость современных компьютерных томографов больше связана не с инженерной сложностью конструкций, а с зашитыми в них нетривиальными математическими алгоритмами, представляющими основную коммерческую тайну.

Современные томографы работают в режиме реального времени и отличаются высокой точностью, выявляя малейшие отличия в плотности исследуемых тканей (порядка долей процента).

Однако применение рентгеновской компьютерной томографии не всегда показано из–за жёсткости рентгеновского излучения (например, её не рекомендуется применять для диагностирования беременных женщин). В этой ситуации приходится прибегать к менее жёсткому ультразвуковому исследованию. Ультразвук не обладает мощью рентгеновского излучения, переменная плотность тканей приводит к тому, что ультразвуковое излучение распространяется вдоль кривых линий, а не прямых. Но криволинейная задача Радона—задача о восстановлении функции на плоскости по её интегралам вдоль всевозможных кривых определённого вида,— до сих пор остаётся нерешённой. По этой причине приходится пользоваться формулой Радона для прямолинейного случая, что сказывается на точности ультразвуковых томографов по сравнению с их рентгеновскими собратьями. Усовершенствование работы ультразвуковых томографов напрямую зависит от прогресса в решении сформулированной математической задачи.

Криволинейная задача Радона имеет важное значение не только в медицине, но и, например, в геологии, где она возникает при сейсморазведке полезных ископаемых. Допустим, требуется найти рудное тело, находящееся на большой глубине. С этой целью на земной поверхности производится серия микровзрывов, эффект от которых фиксируется прилегающими сейсмическими станциями. По скорости распространения сейсмических волн можно получить данные для постановки криволинейной задачи Радона. Её решение в этом случае позволило бы локализовать разыскиваемое полезное ископаемое. Таким образом, и в случае сейсморазведки дальнейший прогресс зависит от решения криволинейной задачи Радона.

Приведено только два примера использования математических методов томографии — в медицине и геологии. На самом деле, таких применений намного больше.

Cформулированные задачи относятся к области математики, называемой интегральной геометрией. В этой науке остается ещё много нерешённых задач, но можно не сомневаться, что любой прогресс в их решении найдёт важные практические применения.

Инструментарий инженера

Для геометра математика сама по себе есть конечная цель, для инженера — это есть средство, это есть инструмент такой же, как штангель, зубило, ручник, напильник для слесаря или полусаженок, топор и пила для плотника.

Инженер должен по своей специальности уметь владеть своим инструментом, но он вовсе не должен уметь его делать; плотник не должен уметь выковать или наварить топор, но должен уметь отличить хороший топор от плохого; слесарь не должен уметь сам насекать напильник, но должен выбрать тот напильник, который ему надо.

Так вот геометра, который создает новые математические выводы, можно уподобить некоему воображаемому универсальному инструментальщику, который готовит на склад инструмент на всякую потребу; он делает всё, начиная от кувалды и кончая тончайшим микроскопом и точнейшим хронометром. Геометр создает методы решения вопросов, не только возникающих вследствие современных надобностей, но и для будущих, которые возникнут, можеть быть, завтра, может быть, через тысячу лет.

Вообразите же теперь инженера, вошедшего в этот склад и желающего в нём найти нужный ему инструмент. Он прежде всего будет поражён огромным, подавляющим количеством всего накопленного за 2500 лет материала, его изумительным разнообразием. При более внимательном рассмотрении он заметит среди массы других вещей, кажущихся простыми, и некоторые сложнейшие аппараты непонятного ему назначения, но изумительные по отделке их многочисленных деталей, по тщательной их пригонке, да к тому же оправленные в серебро и золото.

Среди аппаратов новейшего изготовления он увидит множество приборов, служащих для самой точной, самой тщательной отделки изделий, т.е. множество разных шаберов и шлифовальных станков. Заметит он и много устарелого, вышедшего, из употребления, местами будет попадаться и просто разный хлам.

Но ведь инженер пришёл сюда не затем, чтобы любоваться неисчислимыми сокровищами: не золото и серебро ему нужны, а быстрорежущая сталь, ему нужен не столько шабер, сколько грубая обдирка, грубое надёжное зубило, ведь не шабером же будет он выбирать шпунт у ахтерштевня. Присмотревшись ещё ближе, он среди этого бесчисленного разнообразия заметит ряд, видимо, издавна систематически подобранных ассортиментов, остающихся почти неизменными в течение 150 лет, к тому же кладовщик ему подскажет, что их так часто требуют, что и не напасёшься, а за остальным заходят лишь знатоки — мастера и любители.

Не отнестись ли ему с доверием к этим, ещё издавна великими мастерами подобранным ассортиментам, и не следует ли ему воспользоваться этими готовыми и десятилетиями, если не столетиями, испытанными инструментами и научиться ими правильно и искусно владеть, а затем уже, когда он сам станет знатоком и мастером, порыться и в остальных сокровищах и попытаться извлечь из них именно то, что ему надо, не брезгуя и шаберами.

Так вот эти систематические ассортименты — это те курсы, которые вам читают, и те руководства, изучение которых вам рекомендуют, а кладовщики и инструментальщики — это те профессора и руководители, которые вас обучают. Может быть, они сами и не инженеры, но зато они хорошо знают и хорошо владеют вверенным им инструментом, склад свой они изучили и знают, где и что в нём можно найти.

Объём шкурки апельсина

Вы купили апельсин и разрезали его пополам. Чего больше по объёму в представленном на картинке апельсине—кожуры или мякоти?

Вопрос кажется странным, ведь кожура — это тонкий слой, край апельсина (будем считать, что он имеет форму шара). Оказывается, что относительно тонкий слой на границе шара имеет тот же объём, что и вся остальная часть. Например, у апельсина диаметром 10 см, c кожурой толщиной 1 см, почти половина всего объёма — в кожуре!

Давайте проверим. Рассмотрим два шара, радиусов R и r (r < R). Каким должен быть радиус меньшего шара, чтобы его объём составлял половину объёма большого?

Объём шара радиуса R равен Vr = 4/3 πR. Для нахождения r запишем уравнение

Vr=VR−Vr, или 4/3πr=4/3πR−4/3πr.

Из него следует что R^3 = 2r^3, т.е.

r = R/√3 2(кубический корень из 2) ≈ 0,79R ≈ 4/5R .

Таким образом, почти половина объёма шара сосредоточена в слое около поверхности толщиной всего лишь ⅕ радиуса.

Поясним читателю выбор формы уравнения: VR = VR − Vr вместо естественного Vr =2Vr. Это сделано, чтобы напомнить одну идею, часто встречающуюся в геометрии и полезную при решении житейских задач, — фигура, для площади или объёма которой нет готовой формулы, представляется как разность «известных» фигур.

Конический фужер

Как уговорить ребёнка выпить злую микстуру? Можно пойти на «математическую» хитрость, и если она сработает, то в дополнение к порции лекарства ребёнок получит поучительное объяснение.

Нальём микстуру в конический бокал и предложим «больному» выпить половину («среднее дипломатическое» для уговаривающего и сопротивляющегося). Большинство автоматически решит, что

«половина» — это «половина по высоте», и… выпьет ⅞ содержимого бокала, т.е. почти всё!

А чтобы выпить половину бокала, надо отпить столько, чтобы уровень жидкости понизился примерно на ⅕ высоты (точнее, на 1 − √3 2(кубический корень из 2)). Число √3 2 уже встречалось на предыдущей странице, его появление здесь вызвано похожими соображениями, только формулу для объёма шара заменит формула для объёма конуса.

Перечисленные «подходы» к бокалу изображены на рисунках. Несколько «практических» замечаний. Приведённые соотношения действуют в любом коническом фужере, т.к. не зависят от угла конуса.

В математике формулы, связи условий и утверждений в теоремах — часто вещи «обратимые», их можно читать-применять и в одну сторону, и в другую. Так и в нашем примере: приведённые математические соображения позволяют «разумно» обосновать желание выпить больше, чем разрешают.

Формат A4

Каким должно быть отношение сторон прямоугольного листа бумаги, чтобы у половины этого листа было такое же отношение сторон?

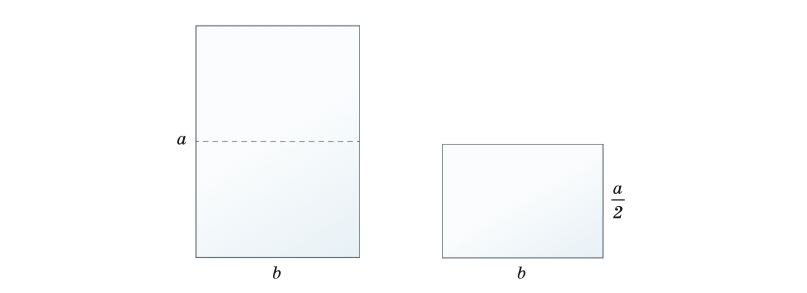
Представим сформулированное условие в виде формулы: a/b=b/a/2.

Отсюда находим отношение сторон a /b=√2.

У листа с таким отношением сторон есть свойство, ценное и в делопроизводстве, и в полиграфии: сложив его пополам, мы получим лист с теми же пропорциями и, значит, также удовлетворяющий сформулированному требованию. С точки зрения геометрии, всё дело в том, что исходный прямоугольник и его «половина» подобны. А если листы подобны, то макет страницы, разработанный для одного из них, можно перенести на второй простым масштабированием.

Стандарты на бумажные форматы, удовлетворяющие сформулированному требованию, были введены в 20-х годах XX века. Применяются серии «А», «B», «С», каждая состоит из последовательности уменьшающихся листов. Выбор самого большого листа в серии («базового», получающего нулевой индекс), связан с той или иной нормировкой. В каждой серии лист с номером n + 1 выглядит как сложенный вдвое лист с номером n.

Число √2, которое теоретически определяет отношение сторон прямоугольных листов всех номеров во всех сериях, является иррациональным. Это означает, что число √2 нельзя представить в виде отношения двух целых чисел, его десятичная запись — бесконечная, непериодическая

√2 = 1,414213562373…

В практической, повседневной жизни приходится использовать рациональные числа. В выборе форматов серий «А», «B», «С» длины сторон листов являются целыми числами (в миллиметрах), эти числа подобраны так, чтобы их отношение было близким к √2.

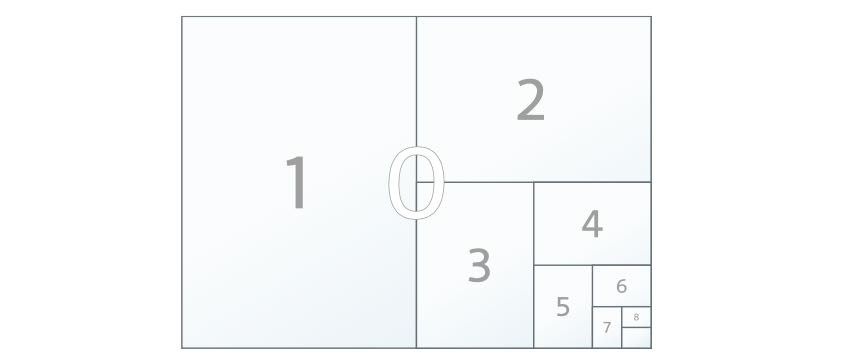
В серии «А» в качестве листа А0 взят лист, имеющий размеры 1189 × 841 мм. Размеры листа были выбраны так, что его площадь с большой точностью равна квадратному метру. В повседневной жизни наиболее часто встречается формат бумаги A4. Длины сторон листа равны 297 и 210 мм, это примерно одна четвёртая часть длин сторон листа A0, площадь листа A4 — примерно 1/16 квадратного метра. При плотности стандартной офисной бумаги 80 грамм на квадратный метр, один лист весит около 5 грамм, а пачка из 500 листов — 2,5 киллограмма.

В серии «B» лист B0 выбран так, что длина его короткой стороны равна 1 метру. Чтобы отношение сторон было близко к √2, в качестве большей стороны листа принято значение 1,414 м. Серия «B» почти не используется в офисной жизни, но имеет ряд специальных применений. Например, паспорт гражданина Российской Федерации имеет формат B7 — 125 × 88 мм, что соответствует рекомендациям, содержащимся в международном стандарте.

Кривая поворота

Прохождение поворота на трассе—демонстрация мастерства пилота в «Формуле 1». Но с этой задачей ежедневно сталкиваются и рядовые водители, и машинисты поездов. А можно ли проектировать дороги так, чтобы уменьшить «стрессы» на поворотах для водителей, пассажиров и даже для техники?

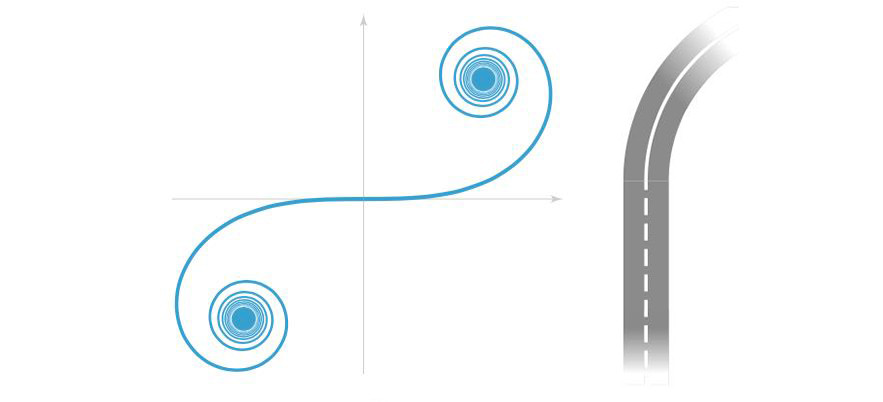
Очевидно, что дорога должна быть гладкой, без изломов. Но для скоростных трасс этого недостаточно.

Представим дорогу в виде прямой, переходящей в дугу окружности. На прямолинейном участке во время движения руль не повёрнут. А при въезде на участок дуги окружности его необходимо резко повернуть. Пассажиры почувствуют толчок. Понятно, что описанный «толчок» при вхождении в такой поворот испытывает и техника. Но если водитель автомашины ещё может попытаться «сгладить» ситуацию за счёт выбора траектории, то машинист поезда такого выбора не имеет, и при неудачном профиле полотна страдать будут все — от пассажиров до рельсов (последние будут быстро изнашиваться).

Итак, непосредственно склеить прямую и окружность в данной ситуации нельзя. Возникает задача расчёта переходной кривой — части дороги, осуществляющей «плавный» (в смысле движения) переход с прямолинейного участка на дугу окружности постоянного радиуса.

В математике у кривых есть важная характеристика — кривизна. У окружности радиуса R кривизна равна 1/R, у прямой кривизна равна 0. Для произвольной гладкой кривой на плоскости кривизна в заданной точке определяется с помощью соприкасающейся окружности, дуга которой в окрестности точки «похожа» на дугу кривой.

Можно ли найти такую переходную кривую, чтобы её кривизна менялась линейно в зависимости от пройденного пути? Тогда при движении с постоянной (по модулю) скоростью руль автомобиля нужно было бы поворачивать равномерно.

Такие кривые существуют, они называются спиралями Корню или клотоидами. Для расчётов спирали Корню сложны, но в построении переходных кривых действительно служат отправной точкой.

Колёсная пара железнодорожных составов

В железнодорожных составах и поездах метро, в отличие от автомобилей, в колёсной паре колёса жёстко сцеплены друг с другом осью и, соответственно, вращаются с одинаковой угловой скоростью. Но при повороте поезда длины путей, пройденных колёсами, будут отличаться: ведь в каждой точке поворота радиус окружности у внешнего рельса чуть больше, чем радиус внутреннего рельса. С другой стороны, по техническим требованиям проскальзывания колёс относительно рельсов быть не должно. Кажется, что отсутствие проскальзывания и разный «пробег» жёстко сцепленных колёс—несовместимые обстоятельства, и что поезда просто не смогут поворачивать. Спасает геометрия: колёса делают не цилиндрическими, а в виде конусов.

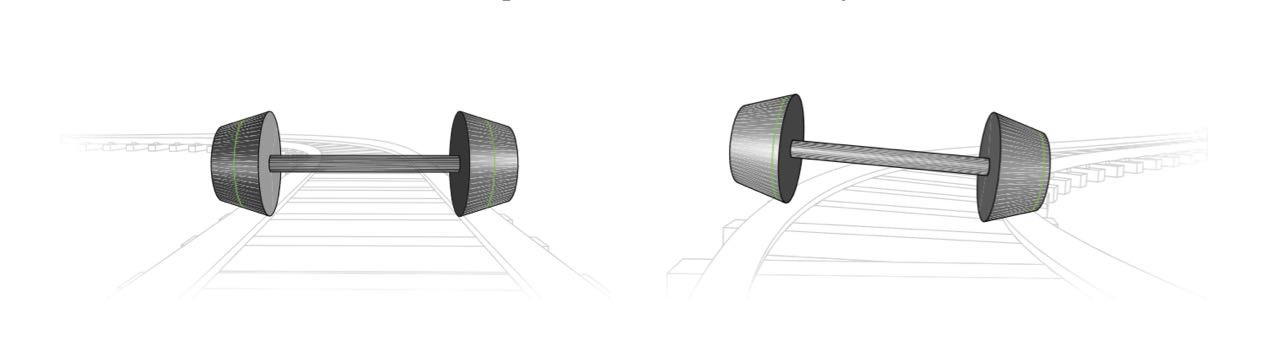
На прямолинейном участке пути такая колёсная пара ведёт себя как цилиндрическая, а на повороте — смещается относительно железнодорожного полотна. В результате внутреннее колесо будет иметь меньший «реальный» радиус, чем внешнее. Смещение и вызванное им изменение радиусов колёс обеспечивают согласованность длин пройденных путей. Удивительно, что геометрия и механика «самостоятельно» определяют эти настройки, без участия человека-машиниста или управляющего механизма.

Конечно, приведённые выше изображения схематичны. У настоящих колёс рабочая поверхность является склейкой двух конусов, да и поверхность рельсов имеет довольно сложный профиль, составленный из дуг нескольких окружностей.

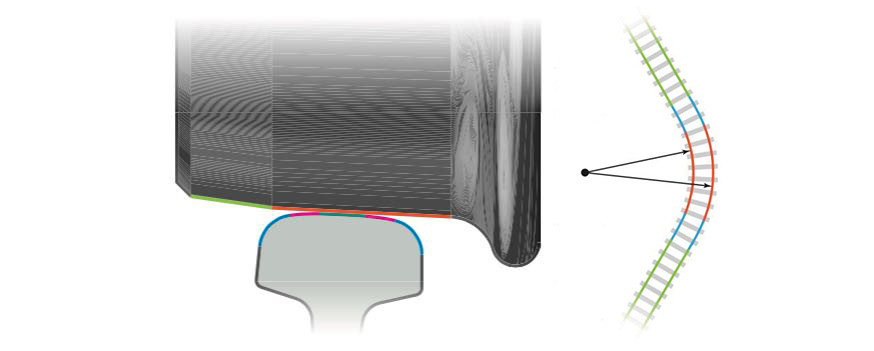
Изложенная геометрическая идея родилась ещё в доэлектрической части XIX века, но верно служит и в компьютерном XXI веке.