Квадратура круга

Простые числа известны давно, но круг — еще более древнее понятие. И именно он породил великую задачу, на решение которой ушло больше 2000 лет. Речь идет об одной из взаимосвязанных геометрических задач, корни которых уходят глубоко в античные времена. Главное действующее лицо этой истории — число π (греческая буква «пи»), знакомое нам по школьной программе в связи с окружностями и сферами. Численно это число равно 3,14159 и еще чуть-чуть; нередко также используется приблизительное значение 22/7. Десятичные знаки в записи π никогда не заканчиваются и не повторяются в одной и той же последовательности снова и снова. Нынешний рекорд вычисления точного значения числа π составляет 10 трлн знаков после запятой. Этот результат Александр Йи и Шигеру Кондо опубликовали в октябре 2011 г. Расчеты такого рода важны как способ испытания быстрых компьютеров или новых, еще более хитроумных методик вычисления числа π, но от численного результата как такового почти ничего не зависит. Причина интереса к числу π не в том, что без него невозможно вычислить длину окружности. Это странное число то и дело мелькает в самых разных областях математики, причем не только в формулах, имеющих отношение к кругам и сферам, и заводит в невероятные дебри. Тем не менее школьные формулы тоже важны, к тому же они отражают древнегреческое происхождение π.

Там одной из величайших проблем считалась нерешенная задача о квадратуре круга. В современном языке эта фраза часто используется иносказательно и означает безнадежное, бессмысленное или тщетное предприятие. Как многие общеупотребительные фразы, берущие начало в научной терминологии, эта с течением времени не раз меняла значение. В греческие времена попытка найти квадратуру круга представлялась вполне разумным начинанием. Разница формы этих фигур — прямые или изогнутые границы — никакого значения не имеет: многие аналогичные задачи решаются. Однако со временем выяснилось, что эта конкретная задача не может быть решена заданными методами. Чтобы это доказать, пришлось проявить изобретательность и сделать серьезные теоретические выкладки, но общую идею доказательства понять все же можно.

В математике под квадратурой круга понимают построение квадрата, равного по площади данному кругу, при помощи традиционных евклидовых методов. Вообще говоря, греческая геометрия допускала и другие методы, поэтому важно сразу определить, какие из них следует использовать. Но тогда неразрешимость задачи говорит только об ограниченности выбранных методов; из нее не следует, что мы не в состоянии определить площадь круга. Просто делать это придется иначе. Доказательство неразрешимости задачи о квадратуре круга помогает понять, почему греческие геометры не смогли найти требуемое построение: его просто не существует. Если разобраться, то именно поэтому им пришлось прибегать к довольно странным, чуть ли не эзотерическим методам. Так что окончательное решение этой задачи, хотя и отрицательное, помогло ученым прояснить довольно серьезную историческую загадку. Оно позволило также больше не терять времени на поиски несуществующего построения — хотя, к сожалению, всегда найдутся те, кто не сможет или не захочет принять окончательный результат, как бы тщательно его ни разжевывали.

В «Началах» Евклида для геометрических построений используются идеальные версии двух математических инструментов: линейки и циркуля. (Поскольку у циркуля две ножки, про него, вероятно, следовало бы говорить циркули, — ведь бумагу мы режем ножницами, а не одним ножницем, но я буду пользоваться традиционной терминологией.) При помощи этих инструментов геометры «чертят» на умозрительном листе бумаги — евклидовой плоскости.

Форма инструментов определяет их возможности. Циркуль представляет собой два прямых жестких стержня, соединенных шарниром. Конец одного стержня заострен, на конце другого закреплен заостренный грифель. При помощи циркуля можно нарисовать круг или часть круга определенного радиуса с центром в определенной точке. Линейка еще проще: у нее есть прямой край, по которому можно провести прямую линию. В отличие от линеек, которые сегодня можно купить в любом канцелярском магазине, линейка Евклида не имеет разметки, и это важное ограничение для математического анализа ее возможностей.

Почему речь идет об идеальных версиях инструментов, понятно: считается, что с их помощью проводятся бесконечно тонкие линии. Более того, все прямые получаются идеально прямыми, а окружности — идеально круглыми. Бумага также идеально плоская и ровная. Еще один ключевой элемент евклидовой геометрии — представление об идеальной точке. Точка ставится на бумаге, но физически такая точка невозможна: она не имеет размера. «Точка, — говорит Евклид в первой фразе своих “Начал”, — это то, что не имеет частей». По описанию она немного напоминает атом или, если вы немного в курсе современной физики, элементарную частицу, но в сравнении с геометрической точкой и атом, и частица — гигантские объекты. Однако в рамках обыденных представлений идеальная точка Евклида, атом и карандашная точка на бумаге одинаково хорошо годятся для геометрических построений.

В реальном мире идеал недостижим, как бы мы ни старались заточить карандаш и какой бы гладкой ни делали бумагу. Но в данном случае идеализм — достоинство, поскольку идеализация значительно упрощает математику. К примеру, пересечение двух реальных карандашных линий представляет собой небольшую размытую область в виде параллелограмма, но математические линии пересекаются исключительно в точке. Откровения, полученные из идеальных окружностей и линий, нередко можно перенести в реальный мир и применить к реальным несовершенным фигурам. Именно так работает волшебство математики.

Две точки определяют единственную прямую, которая через них проходит. Чтобы построить эту прямую, прикладываем нашу идеальную линейку так, чтобы ее сторона проходила через обе точки, и проводим вдоль нее идеальным карандашом. Две точки также определяют круг: выберите одну из точек — она станет центром окружности — и поставьте в нее острие циркуля; затем разведите ножки циркуля так, чтобы кончик грифеля встал на вторую точку. А теперь ведите грифель по дуге, аккуратно удерживая острие в центре. Две прямые определяют единственную точку пересечения — если, конечно, они не параллельны; в этом случае прямые не пересекаются, зато широко распахивается логический ящик Пандоры. Прямая и окружность определяют две точки, если пересекаются, и одну, если прямая лишь касается окружности; если окружность слишком мала, чтобы дотянуться до прямой, пересечения не будет. Точно так же две окружности могут пересекаться в двух точках, в одной или не пересекаться вовсе.

Расстояние — фундаментальная концепция, без которой немыслимо современное прочтение евклидовой геометрии. Расстояние между двумя точками измеряется по прямой, их соединяющей. Евклид, разрабатывая свою геометрию, обходился без явно выраженной концепции расстояния, но он и без этого мог определить, когда два отрезка прямой имеют одинаковую длину. Это очень просто: достаточно поставить ножки циркуля на концы одного отрезка, перенести инструмент ко второму отрезку и посмотреть, встанут ли ножки на его концы. Если встанут, то длины этих отрезков одинаковы; если нет — нет. Эта процедура вовсе не требует измерения реальных длин.

Из этих базовых составляющих геометры могут построить более интересные формы и конфигурации. Три точки определяют треугольник, если только не лежат на одной прямой. Две прямые, пересекаясь, образуют угол. Особенно важен прямой угол, а развернутый угол соответствует двум составленным вместе прямым углам. И так далее и тому подобное, до бесконечности. «Начала» Евклида включают в себя 13 книг и с каждой книгой все глубже зарываются в следствия этих простых начал.

Основное содержание «Начал» — теоремы, строительный материал геометрии. Кроме того, Евклид объясняет, как решать геометрические задачи при помощи «построений», сделанных с применением линейки и циркуля. Как, имея две точки, соединенные отрезком прямой, получить среднюю точку отрезка? Как разделить отрезок на три равные части? Как, имея угол, построить другой угол, равный в точности половине первого? Но некоторые простые построения неожиданно оказались неуловимыми. К примеру, трисекция угла: постройте угол, который ровно втрое меньше заданного. С отрезками такое проходит, но для углов никому так и не удалось отыскать соответствующий метод. С любой степенью приблизительности — да, пожалуйста. Построить точно при помощи циркуля и линейки — нет, увольте. Однако в реальной жизни никому обычно не надо делить угол ровно натрое, так что этот конкретный вопрос не вызвал особых проблем.

Куда больше шума наделало построение, обойтись без которого было никак нельзя: имея заданный круг, построить квадрат той же площади. Это и есть задача о квадратуре круга. С точки зрения греков, если невозможно решить эту задачу, то нельзя и утверждать, что круг вообще имеет площадь.

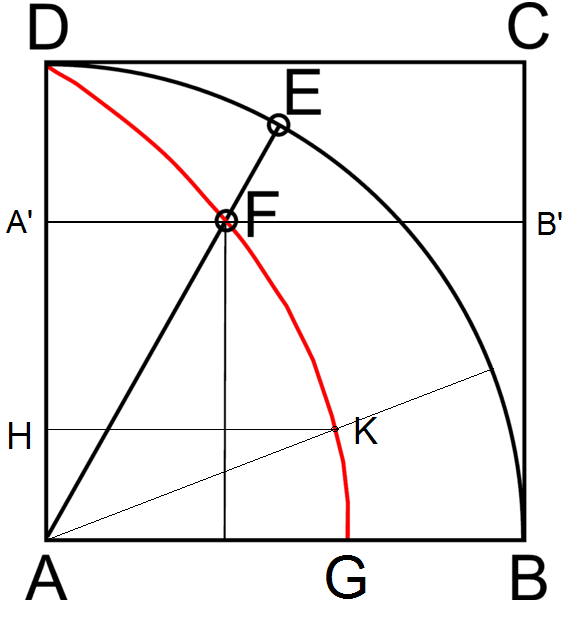
Ну и что, что он очевидно заключает в себе определенное пространство — площадь-то интуитивно определяется по тому, сколько пространства заключает в себе фигура. Евклид и его последователи, в частности Архимед, сошлись на прагматическом решении: они считали, что круг имеет площадь, но построить квадрат той же площади невозможно. О площади круга, конечно, тоже можно кое-что сказать. К примеру, можно доказать со всей логической строгостью, что площадь круга пропорциональна квадрату его диаметра. А вот что невозможно сделать, не решив задачу квадратуры круга, так это начертить отрезок, длина которого будет представлять собой коэффициент этой пропорциональности.

Греки не смогли решить задачу квадратуры круга при помощи линейки и циркуля, им пришлось удовлетвориться другими методами. Один из них воспользовался для этого кривой, получившей название квадратрисы. Судя по всему, позднейшие комментаторы сильно преувеличили значение, которое греческие геометры придавали тому, что всякое построение должно делаться только при помощи линейки и циркуля. По сути, мы даже не можем сказать наверняка, действительно ли греки считали квадратуру круга такой важной задачей. К XIX в., однако, эта проблема приобрела поистине вселенские масштабы. Математика, не способная ответить на такой простой и понятный вопрос, — все равно что повар, не способный сварить яйцо вкрутую.

Формулировка задачи — квадратура круга — звучит очень по-геометрически. Так и есть, это действительно геометрическая задача. А вот решение ее, как оказалось, лежит в области вовсе не геометрии, а алгебры. Дело в том, что решение великих задач часто основывается на выявлении неожиданных связей между разными, на первый взгляд, разделами математики. Связь геометрии и алгебры сама по себе не является чем-то беспрецедентным, но тот факт, что она имеет какое-то отношение к квадратуре круга, был замечен далеко не сразу. А потом, когда связь уже была установлена, возникли чисто технические сложности, и для их разрешения потребовалось привлечь еще один раздел математики — математический анализ. По иронии судьбы первый шаг к прорыву был сделан в четвертой области математики — в теории чисел. В результате была решена геометрическая задача, в решаемость которой греки не поверили бы даже в самых смелых своих мечтах и о которой, насколько нам известно, никогда не думали: задача о построении при помощи циркуля и линейки правильного многоугольника с 17 сторонами.

Звучит дико, особенно если добавить, что для правильных многоугольников с 7, 9, 11, 13 или 14 сторонами ничего подобного не существует, зато многоугольник с 3, 4, 5, 6, 8, 10 и 12 сторонами построить можно. Однако в данном случае за безумием скрывается система, причем такая, что ее выявление заметно обогатило математику.

Начнем с начала: что такое правильный многоугольник? Многоугольник вообще — это фигура, ограниченная прямыми линиями. Многоугольник называется правильным, если все отрезки прямых имеют одинаковую длину и пересекаются под одинаковыми углами. Самый известный пример — квадрат: все четыре его стороны имеют одинаковую длину, а все четыре угла являются прямыми. Существуют и другие фигуры — с четырьмя равными сторонами или с четырьмя равными углами: это, соответственно, ромб и прямоугольник. Только квадрат обладает обоими свойствами одновременно. Правильный трехсторонний многоугольник — это равносторонний треугольник; существуют также правильный пятиугольник, правильный шестиугольник и т. д. Евклид приводит методы построения при помощи циркуля и линейки правильных многоугольников с 3, 4 и 5 сторонами. Кроме того, греки умели последовательно удваивать число сторон, выстраивая многоугольники с 6, 8, 10, 12, 16, 20 и более сторонами. Объединив методы построения правильных многоугольников с 3 и 5 сторонами, они получили правильный 15-угольник. Но на этом продвижение остановилось, и далее, на протяжении 2000 лет, на этом направлении ничего не менялось. Никто не думал, что в этом списке могут появиться многоугольники с еще каким-то числом сторон. Никто даже не задавался этим вопросом: всем казалось, что ничего больше сделать не удастся.

Понадобилось вмешательство одного из величайших математиков всех времен, чтобы обдумать немыслимое, задаться вопросами, задавать которые бесполезно, и получить поистине поразительный ответ. Имя этого математика — Карл Гаусс.

Родился Гаусс в бедной семье в городе Брауншвейге в Германии. Его мать Доротея была неграмотной и не смогла даже записать дату рождения ребенка. Однако она помнила, что было это в 1777 г., за восемь дней до праздника Вознесения. Позже Гаусс сам вычислил точную дату своего рождения при помощи разработанной им формулы расчета дат Пасхи. Отец ученого Гебхард происходил из крестьянской семьи, но зарабатывал на жизнь разной работой: копал канавы, был садовником, уличным мясником, счетоводом похоронной конторы. А их сын оказался вундеркиндом: рассказывали, что уже в трехлетнем возрасте он исправлял отцовские ошибки в арифметике. Его способности, распространявшиеся помимо математики и на языки, побудили герцога Брауншвейгского оплатить обучение мальчика в Брауншвейгском университете. Будучи студентом, Гаусс самостоятельно открыл для себя несколько важных математических теорем, доказанных знаменитыми учеными, такими как Эйлер. Однако его теорема о правильном 17-угольнике грянула как гром среди ясного неба.

К тому времени прошло уже 140 лет с тех пор, как была установлена тесная связь между геометрией и алгеброй. В приложении к «Рассуждению о методе…» Рене Декарт формализовал идею, давно витавшую в воздухе: представление о системе координат. По существу, он взял евклидову девственно чистую плоскость — пустой лист бумаги — и превратил его в лист, расчерченный на квадраты (инженеры и ученые называют такую бумагу миллиметровкой). Для начала нарисуйте на бумаге две прямые линии, горизонтальную и вертикальную. Эти линии называются осями координат. Теперь можно определить положение любой точки на плоскости, задавшись вопросом: как далеко лежит эта точка в направлении вдоль горизонтальной оси и как далеко — вдоль вертикальной (см. рисунок слева). Эти два числа — а они могут быть как положительными, так и отрицательными, — дают исчерпывающее описание точки и называются ее координатами.

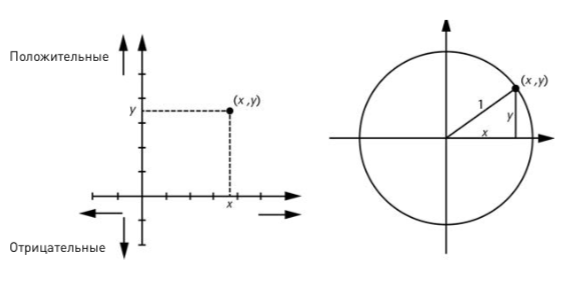
Все геометрические свойства точек, прямых, окружностей и т. д. можно перевести в алгебраические утверждения, связанные с соответствующими координатами. Очень трудно осмысленно говорить об этих связях без использования алгебры — точно так же, как трудно говорить о футболе без использования слова «гол». Поэтому на следующих страницах мне придется привести несколько формул. Они нужны для того, чтобы показать: у главных действующих лиц этой драмы есть имена, и отношения между ними прозрачны. Согласитесь, «Ромео» — это гораздо понятнее, чем «сын итальянского патриция, полюбивший красавицу-дочь заклятого врага своего отца». Наш Ромео будет носить прозаическое имя x, а его Джульетту будут звать y.

В качестве примера того, как геометрия превращается в алгебру, ]унок справа показывает, как найти уравнение окружности единичного радиуса с центром в начале координат, где пересекаются наши две оси. Отмеченная точка имеет координаты (x, y), так что у прямоугольного треугольника на рисунке длина горизонтальной стороны равна x, а вертикальной — y. Самая длинная сторона треугольника представляет собой радиус окружности и, соответственно, равняется единице. Теорема Пифагора гласит, что сумма квадратов двух координат равняется 1. В символьном виде это звучит так: точка с координатами x и y лежит на окружности тогда и только тогда, когда ее координаты удовлетворяют условию x2 + + y2 = 1. Символьная характеристика окружности получилась краткой и точной; она наглядно показывает, что речь в данном случае действительно идет об алгебре. И наоборот, любая алгебраическая характеристика пары чисел, любое уравнение с участием x и y можно интерпретировать как геометрическое утверждение о точках, прямых, окружностях или более сложных кривых.

Фундаментальные алгебраические уравнения включают, в частности, многочлены — комбинации различных степеней неизвестной величины x, где каждая степень x умножается на некое число, называемое коэффициентом. Наибольшая степень x есть степень многочлена. К примеру, уравнение

x4 — 3×3 — 3×2 + 15x — 10 = 0

содержит многочлен, начинающийся с x4, т.е. четвертой степени. Коэффициенты здесь равны 1, –3, –3, 15 и –10. У этого уравнения четыре различных решения: x = 1, 2, 5 и 5 . Для этих чисел левая часть уравнения равняется нулю, т.е. правой части. Многочлены первой степени, такие как 7x + 2, называются линейными и содержат только первую степень неизвестного. Уравнения второй степени, такие как x2 — 3x + + 2 = 0, называются квадратными и содержат вторую степень неизвестного — квадрат. Уравнение окружности содержит вторую переменную y. Однако, если у нас есть второе уравнение, связывающее x и y, к примеру уравнение какой-нибудь прямой, мы можем выразить в нем y через x и преобразовать уравнение окружности так, чтобы оно содержало только x. Это новое уравнение говорит нам о том, где прямая пересекается с окружностью. В данном случае новое уравнение является квадратным и имеет два решения. Так алгебра отражает геометрию, в которой прямая пересекает окружность в двух вполне конкретных точках.

Это свойство алгебры очень существенно влияет на геометрические построения, сделанные при помощи линейки и циркуля. Любое подобное построение, каким бы сложным оно ни было, состоит из последовательности простых шагов. Каждый шаг дает новые точки в местах, где пересекаются две прямые, две окружности или прямая и окружность. Каждая из этих прямых и окружностей определяется ранее построенными точками. Переводя геометрию на язык алгебры, можно доказать, что алгебраическое уравнение, соответствующее пересечению двух прямых, обязательно линейное, а пересечению прямой и окружности или двух окружностей — квадратное. Причина в том, что уравнение окружности содержит x2, но не содержит более высоких степеней x. Поэтому каждый отдельный этап построения соответствует решению уравнения первого или второго порядка, не выше.

Более сложные построения представляют собой последовательности этих базовых операций. Некоторое количество алгебраических преобразований позволяет нам сделать вывод, что каждая координата любой точки, которую можно получить геометрическим построением при помощи линейки и циркуля, является решением полиномиального уравнения с целыми коэффициентами, степень которого представляет собой одну из степеней двойки. Это значит, что степень уравнения должна быть равна одному из чисел 1, 2, 4, 8, 16 и т. д. Это необходимое условие существования такого построения. При должном старании из него можно извлечь точную характеристику, которой должен обладать правильный многоугольник, чтобы его можно было построить. Внезапно из сложной геометрической паутины появляется на свет аккуратное алгебраическое условие, причем применимое к любому построению. Необязательно даже знать, что при этом строится: достаточно, чтобы при построении использовались только линейка и циркуль.

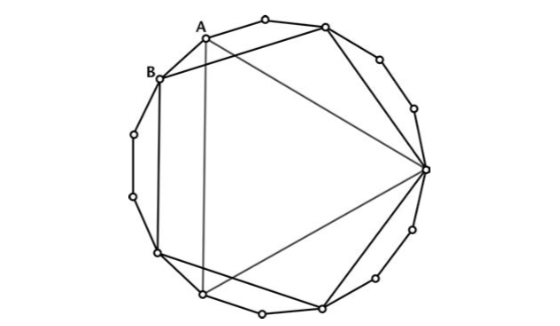
Гаусс был знаком с этой элегантной идеей. Он знал также (к такому выводу пришел бы любой компетентный математик), что вопрос о том, какой правильный многоугольник можно построить при помощи линейки и циркуля, сводится к частному случаю, в котором многоугольник имеет простое число сторон. Чтобы понять, почему так происходит, представьте себе составное число, к примеру 15, т. е. 3 × 5. Любое гипотетическое построение правильного 15-угольника автоматически даст нам правильный же треугольник (возьмите каждую пятую вершину) и пятиугольник (каждую третью), как на рисунке. Приложив еще немного усилий, можно так скомбинировать построения для трехи пятиугольников, чтобы получить в результате 15-угольник. Числа 3 и 5 — простые, и к ним приложима та же общая идея. Так что Гаусс сосредоточился на многоугольниках с простым числом сторон и задался вопросом о том, на что похоже нужное уравнение. Ответ оказался удивительно изящным. Так, построение правильного пятиугольника эквивалентно решению уравнения x5 — 1 = 0. Замените 5 любым другим простым числом — и соответствующее утверждение тоже будет истинным.

Степень этого многочлена — 5, и это не степень двойки, о которой я говорил; тем не менее построить правильный пятиугольник можно. Гаусс быстро определил, почему: это уравнение раскладывается на две части — первого и четвертого порядка. И 1, и 4 являются степенями двойки; оказывается к тому же, что ведущую роль здесь играет уравнение четвертой степени. Чтобы понять, почему нам следует связать это уравнение с геометрией, придется привлечь новый тип числа, который обходит вниманием школьная математика, но без которого на любом более высоком уровне не обойтись. Речь идет о комплексных числах; их определяющим свойством является то, что в системе комплексных чисел из –1 можно извлечь квадратный корень.

Обычное «действительное» число может быть положительным и отрицательным, но его квадрат в том и другом случае положителен, так что –1 не может быть квадратом какого бы то ни было действительного числа. В некоторых случаях это сильно мешает; математики даже изобрели новый тип «воображаемого», или «мнимого», числа, квадрат которого равен –1. Нужно было как-то обозначить это новое число, для чего воспользовались первой буквой слова imaginary (воображаемый) — i. Обычные алгебраические операции — сложение, вычитание, умножение, деление — привели к возникновению комбинаций действительных и мнимых чисел, таких как 3 + 2i. Такие числа называют комплексными, что вовсе не означает «сложные», а просто указывает на то, что они состоят из двух частей: 3 и 2i. Если действительные числа располагаются на известной числовой прямой, как числа на линейке, то комплексные числа лежат на числовой плоскости, на которой мнимая ось располагается под прямым углом к действительной, а вместе они образуют систему координат (см. рисунок, слева).

Уже 200 лет математики считают комплексные числа фундаментальной концепцией своей науки. Мы сегодня признаем, что логически комплексные числа имеют ту же основу, что и более знакомые «действительные» — ведь те тоже, подобно всем математическим структурам, представляют собой абстрактное понятие, а не реальную физическую вещь. Комплексные числа широко использовались еще до Гаусса, но их статус оставался неясным, пока Гаусс и другие математики не сорвали с них завесу тайны, раскрыв неожиданную и парадоксальную причину их привлекательности: несмотря на загадочность и неясный смысл, комплексные числа ведут себя гораздо лучше действительных. Они внесли недостающую составляющую, которой не хватало действительным числам, — обеспечили любому алгебраическому уравнению полный набор решений.

Простейший пример — квадратные уравнения. Одни из них имеют по два действительных решения, другие — не имеют ни одного. К примеру, решениями уравнения x2 — 1 = 0 являются 1 и –1, а уравнение x2 + 1 = 0 решений не имеет. Промежуточное положение занимает x2 = 0, единственное решение которого равно 0, но в некотором смысле это единственное решение «повторяется дважды». Если же мы разрешим комплексные решения, то окажется, что x2 + 1 = 0 тоже имеет два решения: i и –i. Гаусс не стеснялся пользоваться комплексными числами; мало того, его докторская диссертация содержала первое логически безупречное доказательство фундаментальной теоремы алгебры: число комплексных решений любого полиномиального уравнения (если корректно посчитать кратные корни) равняется степени уравнения. Поэтому квадратные уравнения (второй степени) всегда имеют по два комплексных решения, кубические (третьей степени) — по три и т. д.

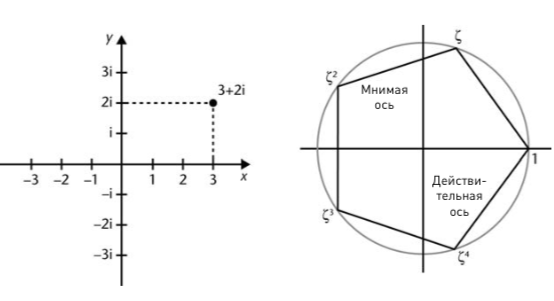
Уравнение x5 — 1 = 0, определяющее, как я уже сказал, правильный пятиугольник, — это уравнение пятой степени, поэтому и комплексных решений у него пять. Действительное решение одно: x = 1. Где же остальные четыре? Они представляют собой четыре вершины правильного пятиугольника на комплексной плоскости, притом что x = 1 — это пятая вершина (см. рисунок, справа). Это соответствие — удачный пример математической красоты: элегантная геометрическая фигура становится элегантным уравнением.

Книгу Иэна Стюарта «Величайшие математические задачи» можно приобрести на сайте издательства.