Ингрид Добеши. Математические тайны Big Data


Ингрид Добеши — профессор математики и прикладной математики в Принстонском университете. В этой небольшой статье продолжает длящуюся рефлексию над Big Data, выбирая для нее перспективу прикладной математики, и вынужденно признается, что несмотря на успешное применение некоторых методов, мы с трудом (если вообще) объясняем себе их природу и значение. Так, например, своего рода «принцип достаточного основания», которым — по Добеши — руководствуются прикладные математики, то ли дает эпистемические сбои, то ли вообще не работает в области Big Data. Тут Добеши надеется на теоретическую помощь чистой математики, что, по-моему, сомнительно, так как речь идет о концептуальных схемах. В общем, где математики опускают руки — там простор для философской и любой другой гуманитарной (в нормальных ее изводах) рефлексии.
Статья опубликована 3 декабря 2015 года в Quanta Magazine
Во время ужина, который я посетила несколько лет назад, известный специалист по дифференциальной геометрии Эудженио Калаби поделился со мной своим остроумным разделением чистой и прикладной математики. Застряв на решении определенной задачи чистый математик обычно решает сузить проблему, чтобы в дальнейшем избежать препятствий. Прикладной математик, оказавшись в тупике, интерпретирует ситуацию как индикатор того, что пора подучить математику и найти инструменты получше.
Мне всегда нравилась эта точка зрения. Она объясняет, как ученые, занимающиеся прикладной математикой, всегда будут нуждаться в использовании новых понятий и структур, постоянно разрабатываемых более фундаментальной математикой. Сегодня это особенно очевидно в продолжающейся попытке понять Big Data — массивы данных, которые являются слишком большими или сложными, чтобы быть понятыми с помощью традиционных техник обработки данных.
Наше нынешнее понимание многих техник, являющихся центральными в продолжающейся революции Big Data, является — в лучшем случае — неадекватным. Давайте рассмотрим самый простой пример, пример управляемого обучения, используемого Google, Facebook и Apple для создания технологий распознавания голоса и изображений с почти человеческой точностью. Эти системы начинают с массивного корпуса обучающих выборок, — миллионов и миллиардов изображений и записей голоса — используемых для того, чтобы обучить глубокую нейронную сеть обнаруживать статистические закономерности. Как и в других областях машинного обучения, надежда на то, что компьютеры смогут распоряжаться достаточным количеством данных, чтобы «научиться» выполнять задание. Вместо того, чтобы запрограммировать их, введя детальные шаги, необходимые для процесса решения, компьютерам дают следовать алгоритмам, которые постепенно приводят их к фокусировке на соответствующих паттернах.
Математически говоря, в эти системы управляемого обучения вводится громадное множество вводных данных и соответствующих им данных на выходе. Цель этого состоит в том, чтобы компьютер выучил функцию, которая в будущем сможет надежно превращать новые вводные данные в правильные данные на выходе. В целях этого, компьютер расщепляет эту загадочную функцию на определенное количество слоев неизвестных функций, называемых сигмоидными функциями. Эти S-образные функции выглядят, как переход с улицы на тротуар: гладкий переход с одного уровня на другой, где ни начальный уровень, ни высота шага, ни ширина области перехода не определены заранее.
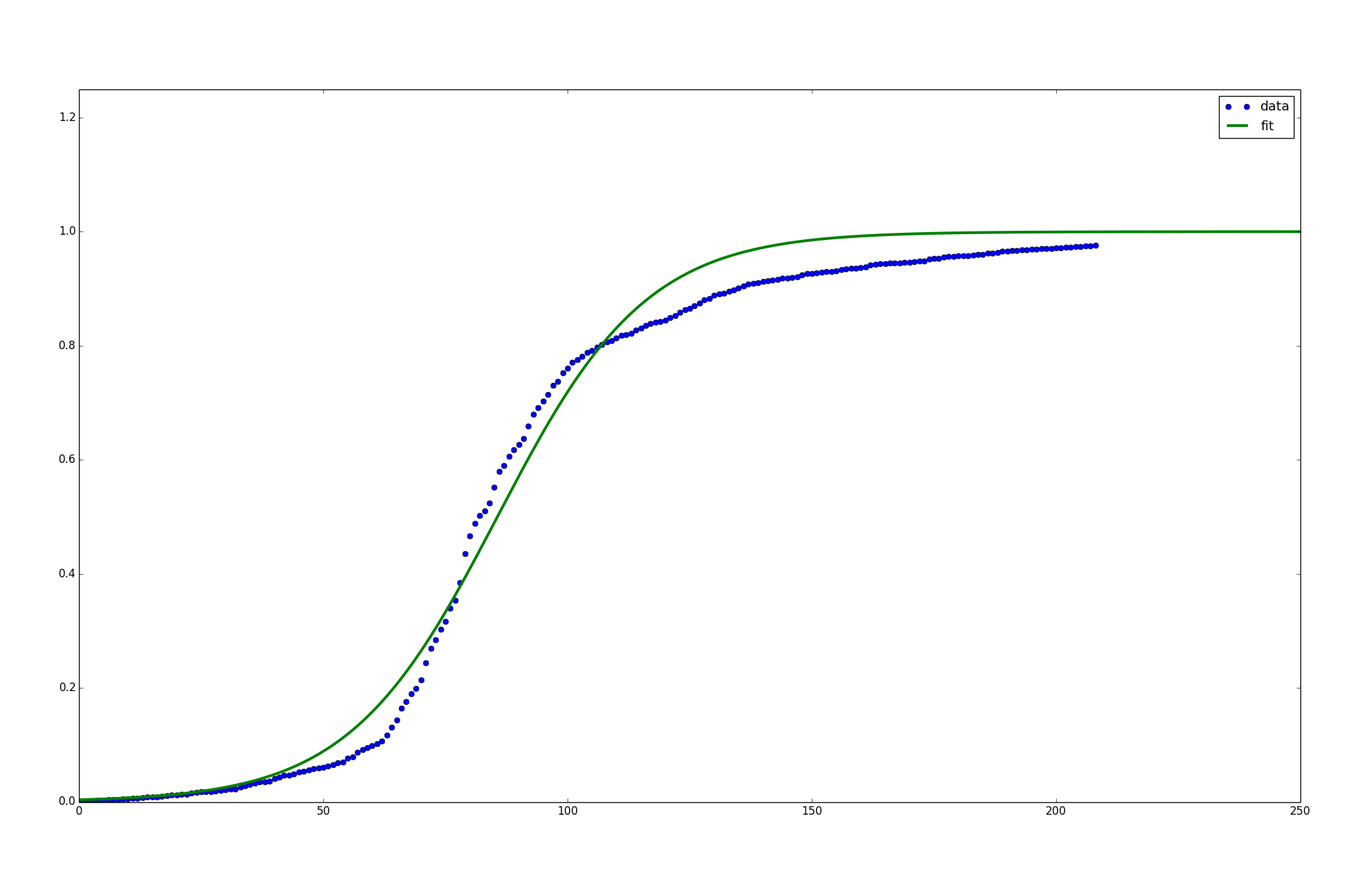
Вводные данные попадают на первый слой сигмоидной функции, выдающий результаты, которые потом можно ввести во второй слой сигмоидной функции и так далее. Это сплетение получающихся функций составляет «сеть» в нейронной сети. «Глубокая» сеть обладает многими слоями.
Десятки лет назад исследователи доказали, что эти сети являются универсальными, имея в виду, что они могут породить все возможные функции. Другие исследователи позже подтвердили некоторое количество теоретических результатов, касающихся уникального соответствия между сетью и порождаемой ей функцией. Но эти результаты предполагают сети, которые могут обладать очень большим количеством слоев с изменениями функций на каждом уровне. На деле нейронные сети используют приблизительно от двух до двух дюжин слоев [1].
Основополагающий принцип многих представителей прикладной математики гласит, что если если нечто математическое действительно работает хорошо, то в основе этого должно лежать математическое основание, а мы должны быть способны понять его. В нашем случае может выйти так, что у нас еще даже нет подходящей математической концептуальной схемы для того, чтобы разобраться в вопросе. Или, если есть, она могла бы быть разработана только в сфере «чистой» математики, еще не проникнув в другие математические дисциплины.
Другой техникой, используемой в машинном обучении, является неуправляемое обучение. Оно используется для обнаружения скрытых связей в больших множествах данных. Допустим, вы являетесь исследователем, желающим больше узнать о человеческих типах личности. Вы удостоились крайне щедрого гранта, позволяющего вам дать 200,000 людям личностный тест на 500 вопросов, ответы в котором распределяются по шкале от 1 до 10. В конечном счете, вы обнаруживаете: у вас 200,000 элементов данных (data points) в 500 виртуальных «измерениях» — одно измерение на каждый уникальный вопрос из теста. Взятые вместе, эти элементы формируют в 500-мерном пространстве «поверхность» меньшего измерения, подобно тому, как простой план отметок высоты элементов горной цепи создает двумерную поверхность в трехмерном пространстве.
То, что вам как исследователю хотелось бы сделать, так это определить эту поверхность меньшего измерения, посредством редукции личностных портретов 200,000 субъектов к их сущностным характеристикам — задача, схожая с нахождением двух переменных, позволяющих определить любую точку на поверхности горной цепи. Вероятно, личностный тест тоже может быть описан простой функцией, связью между некоторым количеством переменных, которое значительно меньше 500. Эта функция, скорее всего, будет отражать скрытую в данных структуру.
За последние пятнадцать (или около того) лет исследователи создали ряд инструментов для изучения геометрии этих скрытых структур. Вы можете, например, построить модель поверхности, используя увеличение для различных точек. В каждой точке (point) вы помещаете на поверхность каплю виртуальных чернил и наблюдаете за их распространением. В зависимости от того, как поверхность искривляется в каждой точке, чернила будут распространяться в определенном, — а не в ином — направлении. Если вы соедините все капли чернил, у вас выйдет неплохая картина того, как выглядит поверхность в целом. И обладая этой информацией, вы обладаете уже не просто коллекцией элементов данных. Теперь вы начнете замечать связи на поверхности, интересные спирали, складки и изгибы. Все это предоставит вам карту для изучения данных.
Эти методы уже дают интересные и полезные результаты, но понадобятся еще многие техники. Прикладным математиками придется много поработать. И перед лицом таких вызовов, они надеются, что многие из их более «чистых» коллег останутся непредвзятыми, будут и дальше следить за тем, что происходит в области, и помогут открытию связей с помощью других математических концептуальных схем. Или, может быть, даже создадут новые.
________________________________________________________________________________
Примечания:
[1] Первоначальная версия этой статьи утверждала, что на практике нейронные сети используют только два или три слоя. Сегодня их количество для наиболее актуальных систем превышает десять слоев. Алгоритм узнавания изображений Google, выигравший недавний ImageNet Large-Scale Visual Recognition Challenge, использует двадцать два слоя.

